��Ŀ����
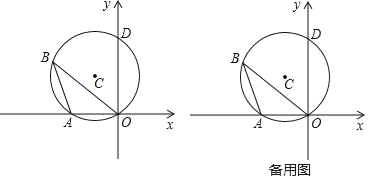
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���D��m��m+8���ڵڶ����ޣ���B��0��n����y���������ϣ���DA��x�ᣬ����ΪA����֪OA��OB��ֵ��2���ı���AOBD�����Ϊ12��

��1����m��n��ֵ��
��2����ͼ2��CΪAO���е㣬DC��AB�ཻ�ڵ�E��AF��BD������ΪF����֤��AF��DE��
��3����ͼ3����G������AD�ϣ���GA��GB��HΪGB�ӳ�����һ�㣬����HAN��y���ڵ�N���ҡ�HAN����HBO����NB��HB��ֵ��
���𰸡���1��![]() ��2�������������3��NB��FB��4���Ƕ�ֵ����������H��GB���ӳ������˶�ʱ��NB��HB��ֵ���ᷢ���仯��
��2�������������3��NB��FB��4���Ƕ�ֵ����������H��GB���ӳ������˶�ʱ��NB��HB��ֵ���ᷢ���仯��
��������
��1���ɵ�D����B��������ı���AOBD�����Ϊ12�����з����飬�ⷽ���鼴�ɣ�
��2���ɣ�1����֪��AD��OA��4��OB��2���������AB��BD��![]() ������SAS��֤��DAC�ա�AOB�����ɵá�AEC��90�������������������ʽ������֤��
������SAS��֤��DAC�ա�AOB�����ɵá�AEC��90�������������������ʽ������֤��
��3��ȡOC��OB������AC�����ݶԳ��Կɵá�ABC����ACB��AB��AC��֤����ABH�ա�CAN�����ɵõ�����.
�⣺��1��������
���![]() ��
��
��2����ͼ2�У�

�ɣ�1����֪��A����4��0����B��0��2����D����4��4����
��AD��OA��4��OB��2��
���ɹ��ɶ����ɵã�AB��BD��![]() ��
��
��AC��OC��2��
��AC��OB��
�ߡ�DAC����AOB��90����AD��OA��
���DAC�ա�AOB��SAS����
���ADC����BAO��
�ߡ�ADC+��ACD��90����
���EAC+��ACE��90����
���AEC��90����
��AF��BD��DE��AB��
��S��ADB��![]() ABAE��
ABAE��![]() BDAF��
BDAF��
��AB��BD��
��DE��AF��
��3���⣺��ͼ��ȡOC��OB������AC�����ݶԳ��Կɵá�ABC����ACB��AB��AC��

��AG��BG��
���GAB����GBA��
��GΪ����AD�ϵ�һ�㣬
��AG��y�ᣬ
���GAB����ABC��
���ACB����EBA��
��180������GBA��180������ACB��
����ABG����ACN��
�ߡ�GAN����GBO��
���AGB����ANC��
����ABG����ACN��
 ��
��
���ABH�ա�ACN��AAS����
��BF��CN��
��NB��HB��NB��CN��BC��2OB��
��OB��2
��
������H��GB���ӳ������˶�ʱ��NB��HB��ֵ���ᷢ���仯��

 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д�