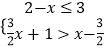题目内容
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y= ![]() (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,
(k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3, ![]() ).
). 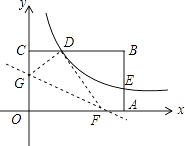
(1)求反比例函数的表达式和m的值;
(2)将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式.
【答案】
(1)解:∵反比例函数y= ![]() (k≠0)在第一象限内的图象经过点E(3,
(k≠0)在第一象限内的图象经过点E(3, ![]() ),
),
∴k=3× ![]() =2,
=2,
∴反比例函数的表达式为y= ![]() .
.
又∵点D(m,2)在反比例函数y= ![]() 的图象上,
的图象上,
∴2m=2,解得:m=1
(2)解:设OG=x,则CG=OC﹣OG=2﹣x,
∵点D(1,2),
∴CD=1.
在Rt△CDG中,∠DCG=90°,CG=2﹣x,CD=1,DG=OG=x,
∴CD2+CG2=DG2,即1+(2﹣x)2=x2,
解得:x= ![]() ,
,
∴点G(0, ![]() ).
).
过点F作FH⊥CB于点H,如图所示.
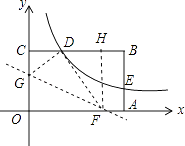
由折叠的特性可知:∠GDF=∠GOF=90°,OG=DG,OF=DF.
∵∠CGD+∠CDG=90°,∠CDG+∠HDF=90°,
∴∠CGD=∠HDF,
∵∠DCG=∠FHD=90°,
∴△GCD∽△DHF,
∴ ![]() =2,
=2,
∴DF=2GD= ![]() ,
,
∴点F的坐标为( ![]() ,0).
,0).
设折痕FG所在直线的函数关系式为y=ax+b,
∴有 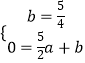 ,解得:
,解得:  .
.
∴折痕FG所在直线的函数关系式为y=﹣ ![]() x+
x+ ![]()
【解析】(1)由点E的坐标利用反比例函数图象上点的坐标特征即可求出k值,再由点B在反比例函数图象上,代入即可求出m值;(2)设OG=x,利用勾股定理即可得出关于x的一元二次方程,解方程即可求出x值,从而得出点G的坐标.再过点F作FH⊥CB于点H,由此可得出△GCD∽△DHF,根据相似三角形的性质即可求出线段DF的长度,从而得出点F的坐标,结合点G、F的坐标利用待定系数法即可求出结论.
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等).

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案