��Ŀ����
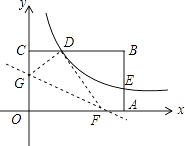
����Ŀ����ͼ1����֪������y=��x2+bx+c��x�ύ��A����1��0����B���㣬����A�ڵ�B����ࣩ����ֱ��AC���ڵ�C��2��3����ֱ��AC�������ߵĶԳ���l�ཻ�ڵ�D������BD��
��1���������ߵĺ�������ʽ���������D�����ꣻ
��2����ͼ2������M��Nͬʱ�ӵ�D����������ÿ��1����λ���ȵ��ٶȷֱ���DA��DB�˶�������MN������DMN��MN���ۣ��õ���D��MN���ж��ı���DMD��N����״����˵�����ɣ����˶�ʱ��tΪ��ֵʱ����D��ǡ������x���ϣ�
��3����ƽ���ڣ��Ƿ���ڵ�P������A�㣩��ʹ����P��B��DΪ��������������ABD���ƣ�ȫ�ȳ��⣩�������ڣ���ֱ��д����P�����꣬�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺����A����1��0����C��2��3������y=��x2+bx+c���ã�
![]() ��
��
��ã� ![]() ��
��
�������ߵĽ���ʽΪy=��x2+2x+3��
��y=��x2+2x+3=����x��1��2+4��
�������ߵĶԳ���Ϊֱ��x=1��
��ֱ��AC�ĺ�������ʽΪy=kx+b��
��A����1��0����C��2��3������y=kx+b���ã�
![]() ��
��
��ã� ![]() ��
��
��ֱ��AC�ĺ�������ʽΪy=x+1��
�֡ߵ�D��ֱ��AC�������ߵĶԳ���Ľ��㣬
��xD=1��yD=1+1=2��
���D��������1��2��
��2��
�⣺�ı���DMD��N�������Σ��������£�
��������y=��x2+2x+3��x�ύ��A��B���㣬
����y=0���é�x2+2x+3=0��
��ã�x1=��1��x2=3��
��A����1��0����B��3��0����
��AD= ![]() =2
=2 ![]() ��BD=
��BD= ![]() =2
=2 ![]() ��AB=1+3=4��
��AB=1+3=4��
��AD2+BD2=AB2��
���ABD�ǵ���ֱ�������Σ�
���DAB=��DBA=45�㣬��ADB=90�㣬
�ɷ��ۿ�֪��D��M=DM��DN=ND�䣬
�֡�DM=DN��
���ı���MDND��Ϊ���Σ�
�ߡ�MDN=90�㣬
���ı���MDND���������Σ�
��DM=DN=t������D����x���ϵĵ�D�䴦ʱ��
���ı���MDND��Ϊ�����Σ�
���D��NB=90�㣬
��Rt��D��NB��D��N=t��BN=2 ![]() ��t��BD��=2��
��t��BD��=2��
��t2+��2 ![]() ��t��2=22��
��t��2=22��
��t1=t2= ![]() ��
��
�������� ![]() sʱ����Dǡ������x���ϵ�D�䴦
sʱ����Dǡ������x���ϵ�D�䴦
��3��
�⣺���ڣ�
��ͼ��
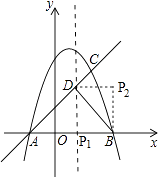
�ɣ�2��֪��ABDΪ����ֱ�������Σ�
�ߡ�PBD���ABD���ƣ��Ҳ�ȫ�ȣ�
���PBD����BDΪб�ߵĵ���ֱ�������Σ�
���P��������1��0����2��3��
����������1�������ô���ϵ������������ߺ�ֱ�ߵĽ���ʽ���Ӷ��ó��Գ�����ֱ�ߵĽ��㣻��2���������߽���ʽ��õ�A��B���꣬��ϵ�D�����֪��ABDΪ����ֱ�������Σ�����DAB=��DBA=45�㡢��ADB=90�㣬�ɷ������ʵ�D��M=DM��DN=ND�䣬�Ӷ��ó��ı���MDND��Ϊ���Σ����ݡ�MDN=90�㼴�ɵ��ı���MDND��Ϊ�����Σ���DM=DN=t����Rt��D��NB��D��N=t��BN=2 ![]() ��t��BD��=2�����ݹ��ɶ������ɵó�t��ֵ����3���ɡ�ABDΪ����ֱ�������μ���PBD���ABD�����Ҳ�ȫ�ȣ�֪��PBD����BDΪб�ߵĵ���ֱ�������Σ����ͼ�μ��ɵô𰸣�
��t��BD��=2�����ݹ��ɶ������ɵó�t��ֵ����3���ɡ�ABDΪ����ֱ�������μ���PBD���ABD�����Ҳ�ȫ�ȣ�֪��PBD����BDΪб�ߵĵ���ֱ�������Σ����ͼ�μ��ɵô𰸣�