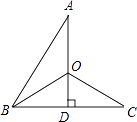��Ŀ����
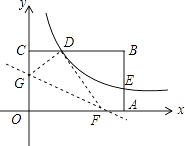
����Ŀ����ͼ1��һ��ϸ��ϵ��һ��С����ƽ���ڰڶ�����֪ϸ�������ҵ�O�����ĵij���Ϊ50���ף�С���ڴ���Bλ��ʱ�ﵽ��͵㣬��С��������Aʱ����͵�Bʱϸ����Ӧ���ɵĽǶȡ�AOB=37�㣮��ȡsin37��=0.6��cos37��=0.8��tan37��=0.75�� 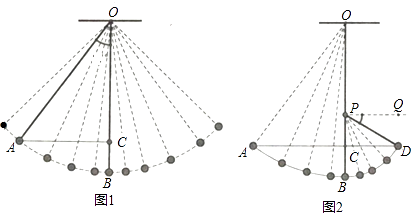
��1�����A���B�ĸ߶Ȳ�BC��ֵ��
��2����ͼ2�����ڵ�O�����·���һ���谭��P����С����������䵽��ʹ����˶��켣�ı䣬��Ϊ��PΪԲ�ģ�PBΪ�뾶�������Ұڶ������ڶ������A��ͬһˮƽ�߶ȵĵ�Dʱ������PD����ϸ����ˮƽ�ߵļнǡ�DPQ=30�㣬��OP�ij��ȣ�
���𰸡�
��1���⣺��AD��OB��
������ɵã���AOB=37�㣬
��CB=OB��OC=OB��OAcos37��=50��50��0.8=10��cm����
��A��B֮��ĸ߶Ȳ�BCΪ10cm
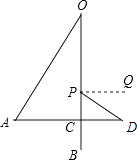
��2���⣺�ɣ�1��֪��B��D�ĸ߶Ȳ�Ҳ��10cm��
��BC=BP��CP=PD��PDcos60��=10��cm����
��ã�PB=20��
��OP=OB��BC=50��20=30��cm����
��OP���ϸ���ij���Ϊ30cm
����������1����������ó�CB=OB��OC=OB��OAcos37�㣬�����ó��𰸣���2����������ó�BP=BP��CP=PD��PDcos60��=10�������ó�PB�ij��������ó��𰸣�

����Ŀ��LED�ƾ��л������ܡ�Ͷ�䷶Χ����Ƶ����ʹ�������ϳ����ص㣬���ճ������У����Ǹ�������LED�Ƶ�ʹ�ã�ijУ��ѧ��ȤС��Ϊ�˽�LED��������ͨ�׳���ݵ�����������������г����飺ij�̳�����һ��30�ߵ�LED���ݺ���ͨ�׳���ݽ������ۣ�������������±���
LED���� | ��ͨ�׳���� | |
���ۣ�Ԫ�� | 45 | 25 |
��ۣ�Ԫ�� | 60 | 30 |

��1�����̳�������LED��������ͨ�׳���ݹ�300����LED���ݰ���۽������ۣ�����ͨ�׳���ݴ�������ۣ����������������ݺ���Ի���3200Ԫ������̳�����LED��������ͨ�׳���ݵ������ֱ�Ϊ���ٸ���
��2�����ڴ����ڼ��������ܿ콫���ֵ��������꣬�����̳��ƻ��ٴι������ֵ���120�����ڲ����۵�����£�������ν�������������������ʱ��������Ҳ����������۵�30%���������ʱ�������ݵ�������Ϊ����Ԫ��