题目内容
【题目】解答题。
（1）计算：|﹣2|﹣ 
+（﹣2）﹣2﹣（ 
）0；
（2）解不等式组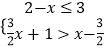 
，并求其最小整数解．
【答案】
（1）解：原式=2﹣ 
+ ﹣1=1
（2）解：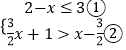 
，
由①得x≥﹣1；由②得x＞﹣5，
∴不等式组的解集为x≥﹣1，
则最小整数解为﹣1
【解析】（1）原式利用绝对值的代数意义，算术平方根定义，零指数幂、负整数指数幂法则计算即可得到结果；（2）分别求出不等式组中两不等式的解集，找出解集的公共部分确定出不等式组的解集，即可确定出最小的整数解．
【考点精析】本题主要考查了一元一次不等式组的解法和一元一次不等式组的整数解的相关知识点，需要掌握解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )；使不等式组中的每个不等式都成立的未知数的值叫不等式组的解，一个不等式组的所有的解组成的集合，叫这个不等式组的解集(简称不等式组的解)才能正确解答此题．
【题目】雾霾天气已经成为人们普遍关注的话题，雾霾不仅仅影响人们的出行，还影响着人们的健康，太原市会持续出现雾霾天气吗？在2016年2月周末休息期间，某校九年级1班综合实践小组的同学以“雾霾天气的主要成因”为主题，随机调查了太原市部分市民的观点，并对调查结果进行了整理，绘制了如下不完整的统计图表，观察并回答下列问题：
类别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 | m |
C | 城中村燃煤问题 | 15% |
D | 其他（绿化不足等） | n |
（1）请你求出本次被调查市民的人数及m，n的值，并补全条形统计图；
（2）若太原市有300万人口，请你估计持有A，B两类看法的市民共有多少人？
（3）学校要求小颖同学在A，B，C，D这四个雾霾天气的主要成因中，随机抽取两项作为课题研究的项目进行考察分析，请用画树状图或列表的方法，求出小颖同学刚好抽到B（汽车尾气排放），C（城中村燃煤问题）的概率．（用A，B，C，D表示各项目）
【题目】有一学校为了解九年级学生某次体育测试成绩，现对这次体育测试成绩进行抽样调查，结果统计如下，其中扇形统计图中C组所在的扇形的圆心角为36° 被抽取的体育测试成绩频数分布表
组别 | 成绩 | 频数 |
A | 20＜x≤24 | 2 |
B | 24＜x≤28 | 3 |
C | 28＜x≤32 | 5 |
D | 32＜x≤36 | b |
E | 36＜x≤40 | 20 |
合计 | a | |
根据上面的图表提供的信息，回答下列问题：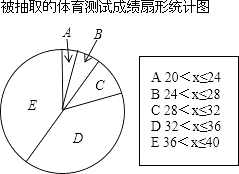
（1）计算频数分布表中a与b的值；
（2）根据C组28＜x≤32的组中值30，估计C组中所有数据的和为；
（3）请估计该校九年级学生这次体育测试成绩的平均分（结果取整数）．