题目内容
【题目】已知点 A、B 在数轴上分别表示有理数 a、b.
(1)对照数轴,填写下表:

(2)若 A、B 两点间的距离记为 d,试问 d 和 a、b(a<b)有何数量关系?数学式子表示.
(3)求所有到数 5 和-5 的距离之和为 10 的整数的和,列式计算.
(4)若点 C 表示的数为 x,当点 C 在什么位置时,|x+1|+|x﹣2|取得的值最小.
【答案】(1)填表如下:
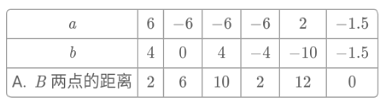
(2)d和a、b之间有的数量关系:d=|ab|;(3) 0;(4) 2,6,10,2,12,0.
【解析】
(1)根据各数据分别计算即可得解;
(2)根据计算结果列出算式即可;
(3)求出-5到5的距离正好等于10可知-5到5之间的所有整数点都可以,然后求解即可;
(4)根据数轴,求出-1到2的距离即为所取得的最小值.
(1)|6-4|=2,|-6-0|=6,|-6-4|=10,|2-(-10)|=12.
填表如下:
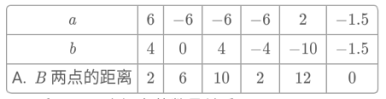
(2)d和a、b之间有的数量关系:d=|ab|;
(3)∵5(5)=5+5=10,
∴点P为5、4、3、2、1、0、1、2、3、4、5,
54321+0+1+2+3+4+5=0;
(4)∵1到2的距离是2(1)=2+1=3,
∴点C在1到2之间时,|x+1|+|x2|取得的值最小,最小值是3.
故答案为:2,6,10,2,12,0.

练习册系列答案
相关题目