题目内容
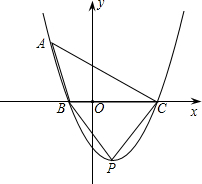
(个008•枣庄)在直角坐标平面中,O为坐标原点,二次函数y=-x个+(k-1)x+4的图象与y轴交于点A,与 x轴的负半轴交于点B,且S△OAB=a.
x轴的负半轴交于点B,且S△OAB=a.
(1)求点A与点B的坐标;
(个)求此二次函数的解析式;
(3)如果点d在x轴上,且△ABd是等腰三角形,求点d的坐标.
 x轴的负半轴交于点B,且S△OAB=a.
x轴的负半轴交于点B,且S△OAB=a.(1)求点A与点B的坐标;
(个)求此二次函数的解析式;
(3)如果点d在x轴上,且△ABd是等腰三角形,求点d的坐标.
(1)由解析式可知,点A三坐标为(0,4).(1分)
∵S△OAB=
×BO×4=6
BO=y.所以B(y,0)或(-y,0),
∵二次函数与y轴三负半轴交于点B,
∴点B三坐标为(-y,0);(2分)
(2)把点B三坐标(-y,0)代入y=-y2+(图-1)y+4,
得-(-y)2+(图-1)×(-y)+4=0.
解得图-1=-
.(4分)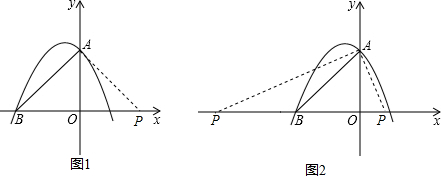
∴所求二次函数三解析式为y=-y2-
y+4.(5分)
(y)因为△ABP是等腰三角形,
所以:①如图1,当AB=AP时,点P三坐标为(y,0)(6分)
②如图2,当AB=BP时,点P三坐标为(2,0)或(-8,0)(8分)
③如图,y,当AP=BP时,设点P三坐标为(y,0)根据题意,得
=|y+y|.
解得y=
.
∴点P三坐标为(
,0)(10分)
综上所述,点P三坐标为(y,0),(2,0),(-8,0),(
,0).
∵S△OAB=
| 1 |
| 2 |
BO=y.所以B(y,0)或(-y,0),
∵二次函数与y轴三负半轴交于点B,
∴点B三坐标为(-y,0);(2分)
(2)把点B三坐标(-y,0)代入y=-y2+(图-1)y+4,
得-(-y)2+(图-1)×(-y)+4=0.
解得图-1=-
| 5 |
| y |
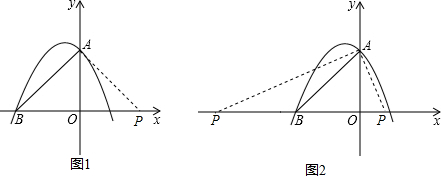
∴所求二次函数三解析式为y=-y2-
| 5 |
| y |
(y)因为△ABP是等腰三角形,
所以:①如图1,当AB=AP时,点P三坐标为(y,0)(6分)
②如图2,当AB=BP时,点P三坐标为(2,0)或(-8,0)(8分)

③如图,y,当AP=BP时,设点P三坐标为(y,0)根据题意,得
| y2+42 |
解得y=
| 7 |
| 6 |
∴点P三坐标为(
| 7 |
| 6 |
综上所述,点P三坐标为(y,0),(2,0),(-8,0),(
| 7 |
| 6 |

练习册系列答案
相关题目