题目内容
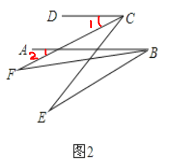
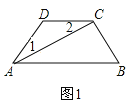
【题目】 (1)、如图，AC平分∠DAB，∠1=∠2，试说明AB与CD的位置关系，并予以证明；
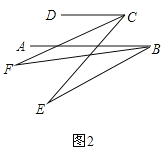
（2）如图，在（1）的条件下，AB的下方两点E，F满足：BF平分∠ABE，CF 平分∠DCE，若∠CFB=20°，∠DCE=70°，求∠ABE的度数
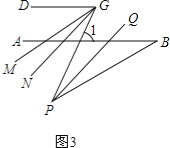
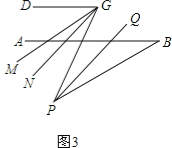
（3）在前面的条件下，若P是BE上一点；G是CD上任一点，PQ平分∠BPG，PQ∥GN，GM平分∠DGP，下列结论：①∠DGP﹣∠MGN的值不变；②∠MGN 的度数不变．可以证明，只有一个是正确的，请你作出正确的选择并求值．
【答案】(1)、AB∥CD；理由见解析；(2)、30°；(3)、①∠DGP﹣∠MGN的值随∠DGP的变化而变化；②∠MGN的度数为15°不变；证明过程见解析.
【解析】
试题分析：(1)、根据角平分线得出∠1=∠CAB，从而得出∠2=∠CAB，从而说明平行线；(2)、根据角平分线的性质得出∠DCF=
∠DCE=35°，∠ABE=2∠ABF，根据CD∥AB得出∠2=∠DCF=35°，根据∠2=∠CFB+∠ABF，∠CFB=20°得出∠ABF和∠ABE的度数；(3)、根据三角形外角性质得出∠1=∠BPG+∠B，根据角平分线的性质得出∠GPQ=
∠BPG，∠MGP=∠DGP，根据AB∥CD得出∠MGP=（∠BPG+∠B），根据PQ∥GN得出∠NGP=∠GPQ=∠BPG，从而根据∠MGN=∠MGP﹣∠NGP=∠B，从而得出答案.
试题解析：(1)、AB∥CD．
∵AC平分∠DAB， ∴∠1=∠CAB， ∵∠1=∠2， ∴∠2=∠CAB， ∴AB∥CD；
(2)、如图2， ∵BF平分∠ABE，CF平分∠CDE， ∴∠DCF=
∠DCE=35°，∠ABE=2∠ABF， ∵CD∥AB，
∴∠2=∠DCF=35°， ∵∠2=∠CFB+∠ABF，∠CFB=20°， ∴∠ABF=15°， ∴∠ABE=2∠ABF=30°
(3)、如图3，根据三角形的外角性质，∠1=∠BPG+∠B， ∵PQ平分∠BPG，GM平分∠DGP，
∴∠GPQ=
∠BPG，∠MGP=∠DGP， ∵AB∥CD， ∴∠1=∠DGP， ∴∠MGP=（∠BPG+∠B），
∵PQ∥GN， ∴∠NGP=∠GPQ=∠BPG， ∴∠MGN=∠MGP﹣∠NGP=（∠BPG+∠B）﹣∠BPG=∠B，
根据前面的条件，∠B=30°， ∴∠MGN=×30°=15°，
∴①∠DGP﹣∠MGN的值随∠DGP的变化而变化；②∠MGN的度数为15°不变．
