��Ŀ����
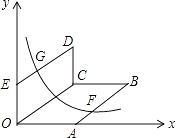
����Ŀ���Ķ����⣺��ͼ1����ƽ����ѡһ����O����һ���з��������Ox����ѡ��һ����λ���ȣ���ôƽ������һ��M��λ�ÿ��ɡ�MOx�Ķ�������OM�ij���mȷ�����������ԣ��ȣ�m����ΪM��ġ������ꡱ����������������ϵ��Ϊ��������ϵ���� Ӧ�ã���ͼ2�ļ�����ϵ�£�����������εı߳�Ϊ2����һ��OA������Ox�ϣ����������εĶ���C�ļ�����Ӧ��Ϊ�� ��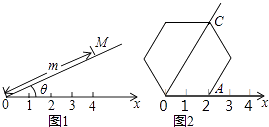
A.��60�㣬4��
B.��45�㣬4��
C.��60�㣬2 ![]() ��
��
D.��50�㣬2 ![]() ��
��
���𰸡�A
���������⣺��ͼ�����������ε�����ΪD������AD�� 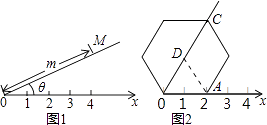
�ߡ�ADO=360���6=60�㣬OD=AD��
���AOD�ǵȱ������Σ�
��OD=OA=2����AOD=60�㣬
��OC=2OD=2��2=4��
���������εĶ���C�ļ�����Ӧ��Ϊ��60�㣬4����
��ѡ��A��
���������ε�����ΪD������AD���жϳ���AOD�ǵȱ������Σ����ݵȱ������ε����ʿɵ�OD=OA����AOD=60�㣬�����OC��Ȼ����ݡ������ꡱ�Ķ���д�����ɣ�

��ϰ��ϵ�д�
 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
�����Ŀ