题目内容
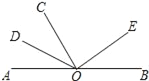
【题目】如图,点O在直线AB上,OD是∠AOC的平分线,射线OE在∠BOC内.
(1)图中有多少个小于180°的角?
(2)若OE平分∠BOC,求∠DOE的度数;
(3)若∠COE=2∠BOE,∠DOE=108°,求∠COE的度数.
【答案】(1)图中有9个小于180°的角;(2)∠DOE=90°;(3)∠COE═72°.
【解析】
(1)根据角的定义,按照一定的规律计数即可;
(2)依据角平分线的定义可知∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,然后逆用乘法的分配律可求得∠DOE=90°;
∠BOC,然后逆用乘法的分配律可求得∠DOE=90°;
(3)设∠BOE=x,然后依据∠DOE=108°列方程求解即可.
(1)图中小于180°的角有∠AOD、∠AOC、∠AOE、∠DOC、∠DOE、∠DOB、∠COE、∠COB、∠EOB共9个;
(2)∵OD平分∠AOC,OE平分∠BOC,
∴![]() ,
,![]() .
.
∵∠AOC+∠BOC=180°,
∴![]() .
.
∴∠DOE=∠COD+∠COE=90°.
(3)设∠BOE=x,
∵∠COE=2∠BOE,∴∠COE=2x,
∴∠AOC=180°﹣3x.
∵OD平分∠AOC,
∴![]() .
.
∵∠COD+∠COE═∠DOE=108°,
∴![]() ,x=36°.
,x=36°.
∴∠COE═72°.

练习册系列答案
相关题目