题目内容
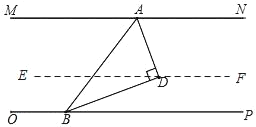
【题目】如图,MN∥OP,点A为直线MN上一定点,B为直线OP上的动点,在直线MN与OP之间且在线段AB的右方作点D,使得AD⊥BD.设∠DAB=α(α为锐角).
(1)求∠NAD与∠PBD的和;(提示过点D作EF∥MN)
(2)当点B在直线OP上运动时,试说明∠OBD﹣∠NAD=90°;
(3)当点B在直线OP上运动的过程中,若AD平分∠NAB,AB也恰好平分∠OBD,请求出此时α的值

【答案】(1)∠NAD+∠PBD=90°;(2)∠OBD﹣∠NAD=90°;(3)α=30°.
【解析】
(1)过点D作EF∥MN,则∠NAD=∠ADE,EF∥OP,依据平行线的性质可得到∠PBD=∠BDE,则∠NAD+∠PBD=∠ADB,最后,依据垂线的定义求解即可;
(2)由(1)得∠NAD=90°-∠PBD,然后结合∠OBD+∠PBD=180°,进行证明即可;
(3)先求得∠OBD的度数(用含α的式子表示),然后再利用(2)中的结论列方程求解即可.
(1)如图,过点D作EF∥MN,则∠NAD=∠ADE.
∵MN∥OP,EF∥MN,
∴EF∥OP.
∴∠PBD=∠BDE,
∴∠NAD+∠PBD=∠ADE+∠BDE=∠ADB.
∵AD⊥BD,
∴∠ADB=90°,
∴∠NAD+∠PBD=90°.
(2)由(1)得:∠NAD+∠PBD=90°,则∠NAD=90°﹣∠PBD.
∵∠OBD+∠PBD=180°,
∴∠OBD=180°﹣∠PBD,
∴∠OBD﹣∠NAD=(180°﹣∠PBD)﹣(90°﹣∠PBD)=90°.
(3)若AD平分∠NAB,AB也恰好平分∠OBD,则有∠NAD=∠BAD=α,∠NAB=2∠BAD=2α,∠OBD=2∠OBA.
∵OP∥MN,
∴∠OBA=∠NAB=2α,
∴∠OBD=4α.
由(2)知:∠OBD﹣∠NAD=90°,则4α﹣α=90°,解得:α=30°.