题目内容
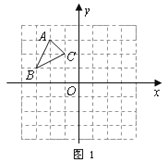
【题目】如图,在△ABC中,AD是BC上的中线,点E在线段AC上且EC=2AE,线段AD与线段BE交于点F,若△ABC对面积为3,则四边形EFDC的面积为__________.

【答案】![]()
【解析】
连接CF,根据CE=2AE,△ABC的面积为3可知S△ABE=![]() ×3=1,S△CEF=
×3=1,S△CEF=![]() ×3=2,S△AEF:S△CEF=1:2,设S△AEF=S,则S△CEF=2S故S△ABF=1-S,则S△BCF=2-2S,设S△ABF=x=1-S,则S△BCF=2x=2-2S,由AD是BC边上的中线可知S△BDF=S△CDF=x,2x=x+3S,即x=3S,所以S△ABC=12S,S四边形EFDC=5S,由此可得出结论.
×3=2,S△AEF:S△CEF=1:2,设S△AEF=S,则S△CEF=2S故S△ABF=1-S,则S△BCF=2-2S,设S△ABF=x=1-S,则S△BCF=2x=2-2S,由AD是BC边上的中线可知S△BDF=S△CDF=x,2x=x+3S,即x=3S,所以S△ABC=12S,S四边形EFDC=5S,由此可得出结论.
连接CF,
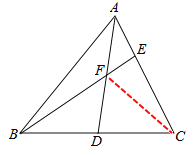
∵CE=2AE,△ABC的面积为3,
∴S△ABE=![]() ×3=1,S△BCE=
×3=1,S△BCE=![]() ×3=2,
×3=2,
S△AEF:S△CEF=1:2,
设S△AEF=S,则S△CEF=2S,
∴S△AFB=1-S,则S△BCF=2-2S,
设S△ABF=x=1-S,则S△BCF=2x=2-2S,
∵AD是BC边上的中线,
∴S△BDF=S△CDF=x,2x=x+3S,即x=3S,
∴S△ABC=12S,S四边形EFDC=5S,
∴![]() .
.
∴S四边形EFDC=![]() =
= ![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目