��Ŀ����
����Ŀ��������y����![]() +bx+c��x�Ḻ�����ڵ�A����y���������ڵ�B��ֱ��AB�Ľ���ʽΪy��
+bx+c��x�Ḻ�����ڵ�A����y���������ڵ�B��ֱ��AB�Ľ���ʽΪy��![]() ��
��
��1����b��c��ֵ��
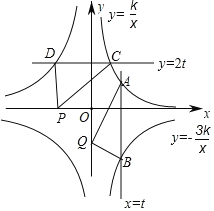
��2��BA��y�ᷭ��180���õ�BA����FΪA��B��һ�㣬BF�Ĵ�ֱƽ���߽�y���ڵ�L��RΪx����һ�㣬BF+OR��2��QR��FL��Q����QR�ij���
��3���ڣ�2���������£�ֱ��LF��x���ڵ�D��EΪ�����ߵ�һ������һ�㣬BE��BD����ABE+��ABD��180�������E�����꣮
���𰸡���1��b��![]() ��c��2
��c��2![]() ����2��QR=��2����3��
����2��QR=��2����3��![]() ��
��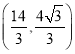
��������
��1�������A��B�����ٴ��������߽���ʽ�������b��c��
��2����LQ�ӳ��߽�x���ڵ�D���������֪LB��LF���Ӷ���ȷ����DLO��60�������ֻ����RD�ij��ȾͿ����ˣ�������������˼�룬��BL��LF��m���ֱ��ʾ��OL��OD��OR���ȣ�OD��OR����RD�ij��ȣ���QR��RD��һ�룮
��3���ɡ�ABE+��ABD��180���Լ�BE��BD���Ե���AB��DE����BP��AB��x���ڵ�P������EP����֤����EDP�ǵȱ������Σ���D�������Ϊn����ɽ�E��������n��ʾ�������ٽ�E��������������߽���ʽ�������n��ֵ��Ҳ�������E�����꣮
��1����ֱ��y��![]() x+2
x+2![]() �ֱ���x�ᡢy�ύ��A��B���㣬
�ֱ���x�ᡢy�ύ��A��B���㣬
��A����2��0����B��0��2![]() ����
����
��������y����![]() +bx+c����A��B���㣬
+bx+c����A��B���㣬
�ཫA��B����������������߽������ã�
��![]() ��2b+c��0��c��2
��2b+c��0��c��2![]() ��
��
��b��![]() ��c��2
��c��2![]() ��
��
�������ߵĽ���Ϊ![]() ��
��
��2��������֪A'��2��0����
��OA'��2��
��tan��A'BO��![]() �����ԡ�OBA'��30����
�����ԡ�OBA'��30����
��LΪBF��ֱƽ�����ϵĵ㣬
��LB��LF��m��
���LFB����LBF��30����
���OLQ��60����BF��![]() m��
m��
��OL��OB��LB��2![]() ��m��
��m��
��LQ���ӳ�����x�ύ�ڵ�D�����LDO��30����
��OD��![]() OL��6��
OL��6��![]() m��
m��
��BF+OR��2��
��OR��2��BF��2��![]() m��
m��
��RD��OD��OR��4��
��RQ��FL��
��QR��![]() RD��2��
RD��2��
��3����ͼ3����GΪAB�ӳ���һ�㣬��BP��AB��x���ڵ�P��
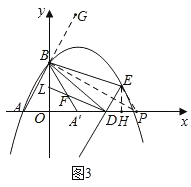
����EP����EH��x����H��
��tan��BAO��![]() ��
��
���BAO��60����
���BPA��30����
�ߡ�ABE+��ABD����ABE+��GBE��180��
���ABD����GBE��
��BD��BE��
���BDE����BED��
�ߡ�ABD+��DBE+��GBE����BDE+��DBE+��BED��180����
���ABD����GBE����BDE����BED��
��AB��DE��
���EDP����BAO��60����
��BP��AB��
��BP��DE��
��PE��PD��
���EDP�ǵȱ������Σ�
��PH��DH��![]() DP��
DP��
��D��������n��0����
��OP��![]() OB��6��
OB��6��
��PD��OP��OD��6��n��
��DH��PH��![]()
��E��![]() ��
��![]() ����
����
��E��������������߽���ʽ���n��4��n��![]() ��
��
��E������Ϊ![]() ��
��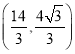 ��
��