题目内容
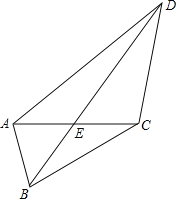
【题目】如图，四边形ABCD中，BD与AC相交于E点，AE＝CE，BC＝AC＝DC，则tan∠ABDtan∠ADB＝_____．
【答案】
【解析】
由BC＝AC＝DC知A、B、D在以C为圆心的圆上，延长AC交⊙C于点F，连接DF、BF，由圆周角定理知∠ADF＝∠ABF＝90°，∠ABD＝∠AFD、∠ADB＝∠AFB，证△ABE∽△DFE、△ADE∽△BFE得
＝
、
＝
，从而由tan∠ABDtan∠ADB＝tan∠AFDtan∠AFB＝
＝
＝
＝
可得答案．
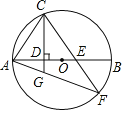
解：∵BC＝AC＝DC，
∴点A、B、D在以C为圆心的圆上，
如图所示，延长AC交⊙C于点F，连接DF、BF、
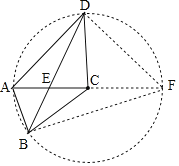
则∠ADF＝∠ABF＝90°，∠ABD＝∠AFD、∠ADB＝∠AFB，
∵∠AEB＝∠DEF、∠AED＝∠BEF，
∴△ABE∽△DFE，△ADE∽△BFE，
∴
、
，
则tan∠ABDtan∠ADB＝tan∠AFDtan∠AFB
＝
＝
＝
＝，
设AE＝CE＝x，则AC＝CF＝2x，
∴AF＝4x，
∴EF＝AF﹣AE＝3x，
则tan∠ABDtan∠ADB＝＝，
故答案为：．
练习册系列答案
名校课堂系列答案
相关题目
