��Ŀ����
����Ŀ����ͼ��1����һ�����¼ܵ�ʵ��ͼ��֧�ܵĻ���ͼ�������Σ�MN�����¼ܵ�һ�����ۣ���P�ڻ���MN�ϡ����ƶ�ʱ�����¼ܿ�����������ʾ��ͼ��ͼ��2����ʾ����֪ÿ�����εı߳���Ϊ20cm����AB=CD=CP=DM=20cm�� 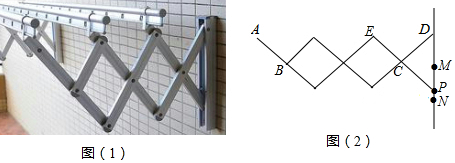
��1������P���»�����N��ʱ����á�DCE=60��ʱ ����MN�ij��ȣ�
�ڴ�ʱ��A��ֱ��DP�ľ����Ƕ��٣�
��2������P���ϻ�����M��ʱ����A������ڣ�1��������������ƶ��ľ����Ƕ��٣� �������ȷ��0.01cm���ο����� ![]() ��1.414��
��1.414�� ![]() ��1.732��
��1.732��
���𰸡�
��1���⣺�ٵ���P���»�����N��ʱ����ͼ1�У���CH��DN��H��
�ߡ�DCE=60�㣬
���DCN=180�㩁��DCE=120�㣬
��CD=CP=20cm����CD=CN=20cm��
���CDN= ![]() ��180�㩁��DCN��=30�㣬
��180�㩁��DCN��=30�㣬
��CH= ![]() CD=10cm��NH=DH=
CD=10cm��NH=DH= ![]() =10
=10 ![]() ��cm����
��cm����
��MN=DN��DM=2DH��DM=20 ![]() ��20��14.6cm��
��20��14.6cm��
���MN�ij���Ϊ14.6cm��
�ڸ������⣬��A��ֱ��DP�ľ�����6CH=6��10=60cm

��2���⣺����P���ϻ�����M��ʱ����ͼ2�У���CMD�ǵȱ������Σ�
���CDM=60�㣬
��CG��DM��G����CG=CDsin60��=20�� ![]() =10
=10 ![]() ��cm����
��cm����
��ʱ��A��ֱ��DP�ľ�����6CG=6��10 ![]() =60
=60 ![]() ��
��
��60 ![]() ��60��43.9cm��
��60��43.9cm��
���A������ڣ�1��������������ƶ��ľ�����43.9cm

����������1���ٵ���P���»�����N��ʱ����ͼ1�У���CH��DN��H����CDN�ǵ��������Σ����NH�ij����ɽ�����⣻�ڸ������⣬��A��ֱ��DP�ľ�����6CH=6��10=60cm����2������P���ϻ�����M��ʱ����ͼ2�У���CMD�ǵȱ������Σ������ʱ��A��ֱ��DP�ľ��뼴�ɽ�����⣻
�����㾫����������Ҫ���������ε����ʵ����֪ʶ�㣬��Ҫ�������ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ�������ȷ�����⣮