题目内容
【题目】如图,在△ABC中,∠ABC=100°,∠ACB的平分线交AB边于点E,在AC边取点D,使∠CBD=20°,连接DE,则∠CED的大小=_____(度).
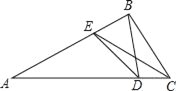
【答案】10.
【解析】
由CE是∠ACB的平分线,可得![]() 由三角形外角的性质,可得∠ADB=∠CBD+∠BCD ①,∠ADE=∠CED+∠ACE ②,继而求得答案.
由三角形外角的性质,可得∠ADB=∠CBD+∠BCD ①,∠ADE=∠CED+∠ACE ②,继而求得答案.
解:延长CB到F,
∵在△ABC中,∠ABC=100°,∠CBD=20°,
∴∠ABF=80°,∠ABD=80°,
∴AB平分∠FBD,
又∵∠ACB的平分线交AB边于点E,
∴点E到边BF,BD,AC的距离相等,
∴点E在∠ADB的平分线上,
即DE平分∠ADB,
∴CE是∠ACB的平分线,
∴![]()
∠ADB是![]() 的外角,∠ADE是
的外角,∠ADE是![]() 的外角,
的外角,
∴∠ADB=∠CBD+∠BCD①,∠ADE=∠CED+∠ACE②
∴①②×2得:2∠CED=∠CBD
∴![]()
故答案为:10.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
【题目】海洋馆的门票价格规定如表:
购票人数(人) | 150人 | 51100人 | 100人以上 |
门票单价(元/人) | 60 | 55 | 50 |
某校七年级一、二两班共102人去游公园,其中一班人数较多,经计算,如果两班都以班为单位分别购买与实际人数相同的票,则一共应付5850元。
请根据以上信息解答下列问题:
①两班各有多少学生?
②如果两班作为一个团体购票,可以节省多少钱?