��Ŀ����
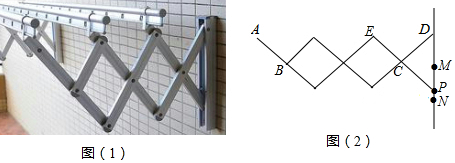
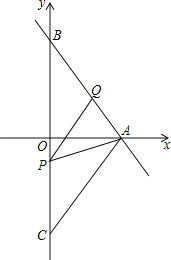
����Ŀ����ͼ1��һ̨������ˮƽ�����ϵıʼDZ����ԣ��������������ͼ2��ʾ�ļ���ͼ�Σ�����ʾ��������IJ��AO�����������IJ��BO����Ϊ24cm����PΪ�۾�����λ�ã�DΪAO���е㣬����PD����PD��AOʱ���Ƶ�PΪ������ӽǵ㡱����PC��BC������C��OB���ӳ����ϣ���BC=12cm�� 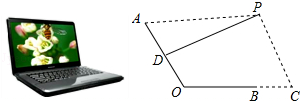
��1����PA=45cmʱ����PC�ij���
��2������AOC=120��ʱ��������ӽǵ㡱P��ֱ��PC�ϵ�λ�ûᷢ��ʲô�仯����ʱPC�ij��Ƕ��٣���ͨ������˵�����������ȷ��0.1cm�����ÿ�ѧ���������ο����ݣ� ![]() ��1.414��
��1.414�� ![]() ��1.732��
��1.732��
���𰸡�
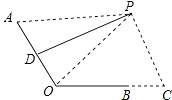
��1���⣺��PA=45cmʱ������PO��
��DΪAO���е㣬PD��AO��
��PO=PA=45cm��
��BO=24cm��BC=12cm����C=90�㣬
��OC=OB+BC=36cm��PC= ![]() =27cm
=27cm
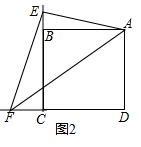
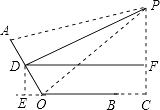
��2���⣺����AOC=120�㣬��D��DE��OC��BO�ӳ�����E����D��DF��PC��F�����ı���DECF�Ǿ��Σ�
��Rt��DOE�У��ߡ�DOE=60�㣬DO= ![]() AO=12��
AO=12��
��DE=DOsin60��=6 ![]() ��EO=
��EO= ![]() DO=6��
DO=6��
��FC=DE=6 ![]() ��DF=EC=EO+OB+BC=6+24+12=42��
��DF=EC=EO+OB+BC=6+24+12=42��
��Rt��PDF�У��ߡ�PDF=30�㣬
��PF=DFtan30��=42�� ![]() =14
=14 ![]() ��
��
��PC=PF+FC=14 ![]() +6
+6 ![]() =20
=20 ![]() ��34.68��27��
��34.68��27��
���P��ֱ��PC�ϵ�λ��������
����������1������PO�������߶δ�ֱƽ���ߵ����ʵó�PO=PA=45cm����OC=OB+BC=36cm��Ȼ�����ù��ɶ����������PC= ![]() =27cm����2����D��DE��OC��BO�ӳ�����E����D��DF��PC��F�����ı���DECF�Ǿ��Σ��Ƚ�Rt��DOE�����DE=DOsin60��=6
=27cm����2����D��DE��OC��BO�ӳ�����E����D��DF��PC��F�����ı���DECF�Ǿ��Σ��Ƚ�Rt��DOE�����DE=DOsin60��=6 ![]() ��EO=
��EO= ![]() DO=6����FC=DE=6
DO=6����FC=DE=6 ![]() ��DF=EC=EO+OB+BC=42���ٽ�Rt��PDF�����PF=DFtan30��=42��
��DF=EC=EO+OB+BC=42���ٽ�Rt��PDF�����PF=DFtan30��=42�� ![]() =14
=14 ![]() ����PC=PF+FC=14
����PC=PF+FC=14 ![]() +6
+6 ![]() =20
=20 ![]() ��34.68��27�����ɵó����ۣ�
��34.68��27�����ɵó����ۣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�