题目内容
【题目】某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).
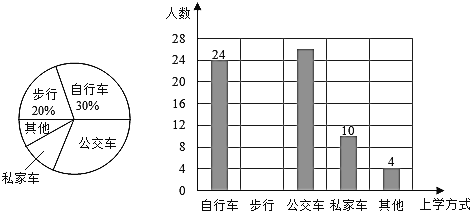
(1)这次调查中,一共抽取了_____名学生;
(2)补全条形统计图;
(3)估计全校所有学生中有多少人乘坐公交车上学?
(4)小明在上学的路上要经过2个路口,每个路口都设有红、黄、绿三种信号灯,假设在各路口遇到信号灯是相互独立的.求小明在上学路上到第二个路口时第一次遇到红灯的概率(请用“画树状图”或“列表”的方法写出分析过程).
【答案】(1)80;(2)见解析;(3)![]() ;(4)
;(4)![]()
【解析】
(1)根据上学方式为“自行车”的学生数除以所占的百分比即可求出调查的学生总数;(2)总人数乘以“步行”的学生所占的百分比求出“步行”的学生人数,补全统计图即可;(3)总人数减去其它四种方式的人数求出上学方式为“公交车”的学生的人数,除以抽查的总人数求出上学方式为“公交车”的学生所占百分比,乘以2400即可得到结果;(4)根据题意画出相应的树状图,得出所有等可能的情况数,找出到第二个路口时第一次遇到红灯的情况数,根据概率公式即可得答案.
(1)24÷30%=80(名);
故答案为:80
(2)被抽到的学生中,步行的人数为![]() ,
,
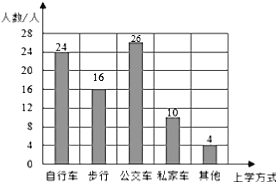
条形统计图如下:
(3)被抽到的学生中,乘公交车的人数为![]() ,
,
∴全校所有学生中乘坐公交车上学的人数约为![]()
(4).画树状图如下:
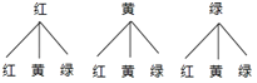
由树状图知,共有9种等可能结果,其中到第二个路口时第一次遇到红灯的结果数为2,所以到第二个路口时第一次遇到红灯的概率为![]()

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案【题目】某商场经营某种品牌的玩具,购进时的单价是40元,根据市场调查:在一段时间内,销售单价是50元时,销售量是600件,而销售单价每涨2元,就会少售出20件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>50),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润ω元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) | ① |
销售玩具获得利润ω(元) | ② |
(2)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于54元,且商场要完成不少于400件的销售任务,求商场销售该品牌玩具获得的最大利润是多少元?