题目内容
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 上一动点,过三点
上一动点,过三点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() .
.
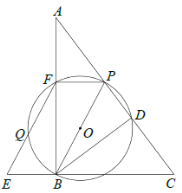
(1)求证:四边形![]() 为平行四边形.
为平行四边形.
(2)当![]() 时,求
时,求![]() 的长.
的长.
(3)在点![]() 整个运动过程中,
整个运动过程中,
①当![]() 中满足某两条线段相等,求所有满足条件的
中满足某两条线段相等,求所有满足条件的![]() 的长.
的长.
②当点![]() 三点共线时,
三点共线时,![]() 交
交![]() 于点
于点![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值. (请直接写出答案)
的值. (请直接写出答案)
【答案】(1)见解析;(2)PD=![]() ;(3)①
;(3)①![]() 或
或![]() 或PF=
或PF=![]() ;②
;②![]()
【解析】
(1)证明两组对边分别平行即可证明四边形FEBP为平行四边形;
(2)①由AC=10,sinC=![]() ,可得BC=6,AB=8,sinA=
,可得BC=6,AB=8,sinA=![]() ,所以AD=ABsin∠ABD=ABsin∠C=8×
,所以AD=ABsin∠ABD=ABsin∠C=8×![]() =
=![]() ,再求得AP=
,再求得AP=![]() ,最后PD=AD﹣AP解答即可;
,最后PD=AD﹣AP解答即可;
②分三种情况讨论:Ⅰ.当PF=PD时,Ⅱ.当QF=PD时,Ⅲ.当QF=PF时,分别解答即可;
③连接FD,求出FD的长,再利用勾股定理求出QF的长.
(1)证明:
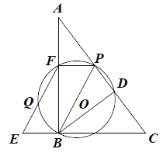
∵![]() ,
,
∴![]() ,
,
∴![]() ,且
,且![]() ,∴
,∴![]() .
.
又∵![]() ,
,
所以四边形![]() 是平行四边形.
是平行四边形.
(2)在![]() 中,∵
中,∵![]() ,
,
∴![]() .
.
∵![]() ,
,
![]() ,
, ![]() .
.
∴![]()
(3)设![]() ,则
,则![]() ,
,
①当![]() 时,如图.
时,如图.
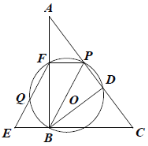
![]()
∴![]()
∴![]() ,
,
∴![]() .
.
②当![]() 时,如图,连结
时,如图,连结![]() .
.
∴![]() ,即
,即![]()
∴![]() ,所以
,所以![]() .
.
由(1)得:四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
在![]() 中,易得
中,易得![]()
∴![]() ,
,
则![]() ,
,
∴![]() .
.
③当![]() 时,如图,连结
时,如图,连结![]() .
.

∵![]()
∴![]() ,
,
∴![]()
在![]() 中,易得
中,易得![]()
∴![]() ,且
,且![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
综上所述,所有满足条件的PF的长有:![]() ;
;
②连接QD,连接FD,交BP于点H.
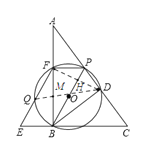
∵Q,O,D三点共线
∴QD为⊙O直径.
∵EF∥BP,O为QD中点,
∴H为DF中点,
∵BP为直径,
∴BP⊥DF,![]() ,
,
∴PF=PD.
设PF=3x,则AF=4x,AP=5x
AD=ABsin∠ABD=ABsin∠C=8×![]() ,
,
∴PD=AD﹣AP=![]() ﹣5x,
﹣5x,
∴3x=![]() ﹣5x,
﹣5x,
∴x=![]() ,PF=PD=
,PF=PD=![]() ,
,
在Rt△ABC中,BD=![]() ,
,
![]()
在Rt△PDB中,DH=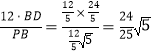 ,
,
∴DF=![]() ,
,
在Rt△DQF中,QF=![]() ,
,
易知△FQM∽△BDM,
∴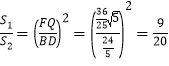 .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案