题目内容
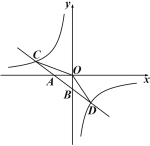
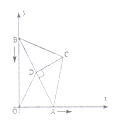
【题目】如图,平行四边形ABCD中,AC,BD为对角线,BC=3,BC边上的高为2,则阴影部分的面积为( )
A. 3B. 4C. 6D. 12
【答案】A
【解析】
由ABCD中,AC.BD为对角线,BC=3,BC边上的高为2,即可求得平行四边形的面积,易证得△AOE≌△COF(ASA),即可得S△AOE=S△COF,同理:S△EOG=S△FOH,S△DOG=S△BOH,即可求得答案.
解:

∵ABCD中,AC.BD为对角线,BC=3,BC边上的高为2,
∴SABCD=3×2=6,AD∥BC,
∴OA=OC,∠OAE=∠OCF,
在△AOE和△COF中,
 ,
,
∴△AOE≌△COF(ASA),
∴S△AOE=S△COF,
同理:S△EOG=S△FOH,S△DOG=S△BOH,
∴S阴影=![]() SABCD=
SABCD=![]() ×6=3.
×6=3.
故选:A.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
【题目】高速公路某收费站出城方向有编号为![]() 的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
收费出口编号 |
|
|
|
|
|
通过小客车数量(辆) | 260 | 330 | 300 | 360 | 240 |
在![]() 五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.
五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.