题目内容
（2012•市中区一模）计算：
（1）计算：
-(
+1)0+(-1)2；．
（2）先化简再计算：
-2x+y，其中x=3，y=2．
（1）计算：
| 18 |
| 3 |
（2）先化简再计算：
| x2-y2 |
| x-y |
分析：（1）原式第一项化为最简二次根式，第二项利用零指数公式化简，第三项（-1）2表示两个-1的乘积，计算后即可得到结果；
（2）原式第一项的分子利用平方差公式分解因式，与分母约分后，合并同类项得到最简结果，然后将x与y的值代入化简后的式子中计算，即可得到原式的值．
（2）原式第一项的分子利用平方差公式分解因式，与分母约分后，合并同类项得到最简结果，然后将x与y的值代入化简后的式子中计算，即可得到原式的值．
解答：解：（1）
-（
+1）0+（-1）2
=3
-1+1
=3
；…（3分）
（2）
-2x+y
=
-2x+y
=x+y-2x+y
=-x+2y，…（5分）
当x=3，y=2时，原式=-3+2×2=-3+4=1．…（7分）
| 18 |
| 3 |
=3
| 2 |
=3
| 2 |
（2）
| x2-y2 |
| x-y |
=
| (x+y)(x-y) |
| x-y |
=x+y-2x+y
=-x+2y，…（5分）
当x=3，y=2时，原式=-3+2×2=-3+4=1．…（7分）
点评：此题考查了分式的化简求值，以及实数的运算，涉及的知识有：二次根式的化简，零指数公式，约分，以及合并同类项，其中分式的加减运算关键是通分，通分的关键是找最简公分母；分式的乘除运算关键是约分，约分的关键是找公因式．
练习册系列答案
相关题目
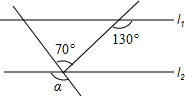（2012•市中区一模）如图，直线l1∥l2，则α=
（2012•市中区一模）如图一次函数
（2012•市中区一模）如图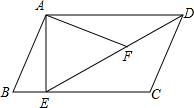，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．
（2012•市中区一模）如图，在直角坐标系中，O是原点，A，B，C三点的坐标分别为A（18，0），B（18，6），C（8，6），四边形OABC是梯形，点P，Q同时从原点出发，分别作匀速运动，其中点P沿OA向终点A运动，速度为每秒1个单位，点Q沿OC，CB向终点B运动，当这两点有一点到达自己的终点时，另一点也停止运动．