题目内容
 (2012•市中区一模)如图,在直角坐标系中,O是原点,A,B,C三点的坐标分别为A(18,0),B(18,6),C(8,6),四边形OABC是梯形,点P,Q同时从原点出发,分别作匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位,点Q沿OC,CB向终点B运动,当这两点有一点到达自己的终点时,另一点也停止运动.
(2012•市中区一模)如图,在直角坐标系中,O是原点,A,B,C三点的坐标分别为A(18,0),B(18,6),C(8,6),四边形OABC是梯形,点P,Q同时从原点出发,分别作匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位,点Q沿OC,CB向终点B运动,当这两点有一点到达自己的终点时,另一点也停止运动.(1)求直线OC的解析式.
(2)设从出发起,运动了t秒.如果点Q的速度为每秒2个单位,试写出点Q的坐标,并写出此时t的取值范围.
(3)设从出发起,运动了t秒.当P,Q两点运动的路程之和恰好等于梯形OABC的周长的一半,这时,直线PQ能否把梯形的面积也分成相等的两部分?如有可能,请求出t的值;如不可能,请说明理由.
分析:(1)O,C两点的坐标分别为O(0,0),C(8,6),利用待定系数法即可求得一次函数的解析式;
(2)当Q在OC上运动时,Q的坐标满足直线OC的解析式,可设Q(m,
m),则OQ就是Q运动的路程,利用勾股定理即可利用t表示出m,从而求得Q的坐标;
当Q在CB上运动时,Q点所走过的路程为2t,求得CQ的长度,即可求得Q的坐标;
(3)当Q点在OC上运动时,P运动的路程为t,则Q运动的路程为(22-t),根据△OPQ的面积等于梯形面积的一半,即可得到一个关于t的方程,根据方程的解得情况即可判断;
当Q在BC上运动时,Q走过的路程为(22-t),根据梯形OCQP的面积等于梯形OABC的面积的一半从而列方程求解.
(2)当Q在OC上运动时,Q的坐标满足直线OC的解析式,可设Q(m,
| 3 |
| 4 |
当Q在CB上运动时,Q点所走过的路程为2t,求得CQ的长度,即可求得Q的坐标;
(3)当Q点在OC上运动时,P运动的路程为t,则Q运动的路程为(22-t),根据△OPQ的面积等于梯形面积的一半,即可得到一个关于t的方程,根据方程的解得情况即可判断;
当Q在BC上运动时,Q走过的路程为(22-t),根据梯形OCQP的面积等于梯形OABC的面积的一半从而列方程求解.
解答:解:(1)∵O,C两点的坐标分别为O(0,0),C(8,6),设OC的解析式为y=kx+b,
将两点坐标代入得:k=
,b=0.
∴y=
x.
(2)当Q在OC上运动时,可设Q(m,
m),依题意有:m2+(
m)2=(2t)2,解得m=
t.
则Q(
t,
t)(0≤t≤5).
当Q在CB上运动时,Q点所走过的路程为2t.
∵OC=10,
∴CQ=2t-10.
∴Q点的横坐标为2t-10+8=2t-2.
∴Q(2t-2,6)(5≤t≤10).
(3)∵梯形OABC的周长为44,当Q点在OC上运动时,P运动的路程为t,则Q运动的路程为(22-t).
△OPQ中,OP边上的高为:(22-t)×
.
∴S△OPQ=
t(22-t)×
,S梯形OABC=
(18+10)×6=84.
依题意有:
t(22-t)×
=84×
.
整理得:t2-22t+140=0.
∵△=222-4×140<0,
∴这样的t不存在.
当Q在BC上运动时,Q走过的路程为(22-t),
∴CQ的长为:22-t-10=12-t.
∴S梯形OCQP=
×6(22-t-10+t)=36≠84×
.
∴这样的t值也不存在.
综上所述,不存在这样的t值,使得P,Q两点同时平分梯形的周长和面积.
将两点坐标代入得:k=
| 3 |
| 4 |
∴y=
| 3 |
| 4 |
(2)当Q在OC上运动时,可设Q(m,
| 3 |
| 4 |
| 3 |
| 4 |
| 8 |
| 5 |
则Q(
| 8 |
| 5 |
| 6 |
| 5 |
当Q在CB上运动时,Q点所走过的路程为2t.
∵OC=10,
∴CQ=2t-10.
∴Q点的横坐标为2t-10+8=2t-2.
∴Q(2t-2,6)(5≤t≤10).
(3)∵梯形OABC的周长为44,当Q点在OC上运动时,P运动的路程为t,则Q运动的路程为(22-t).
△OPQ中,OP边上的高为:(22-t)×
| 3 |
| 5 |
∴S△OPQ=
| 1 |
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
依题意有:
| 1 |
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
整理得:t2-22t+140=0.
∵△=222-4×140<0,
∴这样的t不存在.
当Q在BC上运动时,Q走过的路程为(22-t),
∴CQ的长为:22-t-10=12-t.
∴S梯形OCQP=
| 1 |
| 2 |
| 1 |
| 2 |
∴这样的t值也不存在.
综上所述,不存在这样的t值,使得P,Q两点同时平分梯形的周长和面积.
点评:此题是一次函数与梯形相结合的题目,解答此题的关键是结合图形分别表示出P,Q的坐标,分别求出各点的坐标再计算.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
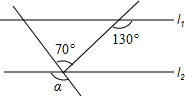 (2012•市中区一模)如图,直线l1∥l2,则α=
(2012•市中区一模)如图,直线l1∥l2,则α=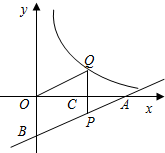 (2012•市中区一模)如图一次函数
(2012•市中区一模)如图一次函数
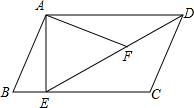 (2012•市中区一模)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(2012•市中区一模)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.