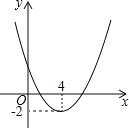
[题目]二次函数y=ax2+bx+c的图象如图.则方程ax2+bx+c=m有实数根的条件是．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】二次函数y=ax2+bx+c（a≠0，a、b、c为常数）的图象如图，则方程ax2+bx+c=m有实数根的条件是．

【答案】m≥﹣2

【解析】

试题分析：由于抛物线y=ax2+bx+c与直线y=m有交点时，方程ax2+bx+c=m有实数根，观察函数图象得到当m≥﹣2时，抛物线y=ax2+bx+c与直线y=m有交点，从而得到方程ax2+bx+c=m有实数根的条件．

解：当抛物线y=ax2+bx+c与直线y=m有交点时，方程ax2+bx+c=m有实数根，

因为直线y=﹣2与抛物线y=ax2+bx+c只有一个公共点，

所以当m≥﹣2时，抛物线y=ax2+bx+c与直线y=m有交点，

即方程ax2+bx+c=m有实数根的条件是m≥﹣2．

故答案为m≥﹣2．

练习册系列答案

课课练与单元测试系列答案

（1）若∠AEF=20°，∠ADE=50°，AC=2，求AB的长度；

（2）求证：AE=AF+BC；

（3）如图2，点F是线段BA延长线上一点，探究AE、AF、BC之间的数量关系，并证明．

（1）若旅游团一天共花去住宿费2140元，那么三人间客房和两人间客房各租住了多少间？

（2）若旅游团一天共花去住宿费m（元），住在三人间的共有n（人），求m与n的函数关式．

（1）若1表示的点与﹣1表示的点重合，则﹣2表示的点与数表示的点重合；

（2）若﹣1表示的点与3表示的点重合，5表示的点与数表示的点重合；

（3）若数轴上A、B两点之间的距离为c个单位长度，点A表示的有理数是a，并且A、B两点经折叠后重合，请写出此时折线与数轴的交点表示的有理数是多少？

A． B． C． D．

（1）分别计算甲、乙两山样本的平均数，并估算出甲、乙两山杨梅的产量总和；

（2）试通过计算说明，哪个山上的杨梅产量较稳定？

（1）求m的值和抛物线的解析式；

（2）求方程x2+bx+c=x+m的解．（直接写出答案）

试题分类