Question

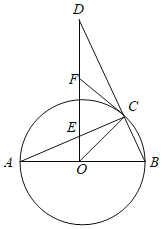
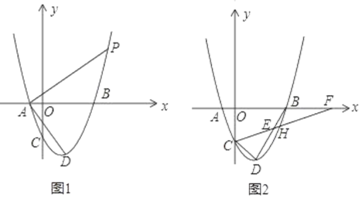
【题目】如图1，已知抛物线y＝x2+mx+m﹣1的顶点为D，交y轴于C点，交x轴于A(x1，0)，B(x2，0)两点，点A在y轴左边，点B在y轴右边，且AB＝4．

（1）求抛物线的解析式；

（2）如图1，AP⊥AD交抛物线于P．求点P的坐标；

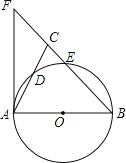
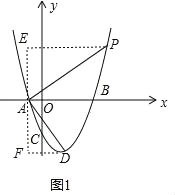
（3）如图2，点H为B，D之间抛物线上一点，直线CH交BD于E，交x轴于F，若S△CDE＝S△BEF，求H点的坐标．

Answer 1

【答案】（1）y＝x2﹣2x﹣3；（2）P(，)；（3）H为(，﹣)

【解析】

（1）由韦达定理得：x1+x2=-m，x1x2=m-1，而x2-x1=4，即：（x1+x2）2-4x1x2=16，即可求解；

（2）如下图，利用△AEP∽△PFE即可求解；

（3）设直线CF的表达式为y=kx-3求出E、F坐标，利用由S△CDE=S△BEF，即可求解．

解：（1）由韦达定理得：x1+x2＝﹣m，x1x2＝m﹣1，

而x2﹣x1＝4，即：（x1+x2）2﹣4x1x2＝16，

解得：m＝﹣2，m＝6（舍去），

故函数的表达式为：y＝x2﹣2x﹣3，

则：A（﹣1，0）、B（3，0）、C（0，﹣3）、D（1，﹣4）；

（2）如下图，过A点作y轴的平行线交过P点与x的平行线与E，交过点D与x轴的平行线与F，

∵AP⊥AD，

∴∠DAF+∠AEP＝90°，∠EPA+∠EAP＝90°，

∴∠EPA＝∠DAF，

∴△AEP∽△PFE，

∴，

设P（m，m2﹣2m﹣3）

其中：PE＝m+1，AF＝4，AE＝m2﹣2m﹣3，FD＝2，代入上式，

解得：m＝，m＝﹣1（舍去），

即：P（，）；

（3）设：直线CF的表达式为y＝kx﹣3…①，

直线BD的方程为：y＝2x﹣6…②，

联立①、②解得E（，），F（，0），

过D点做DM∥y轴，交FC于H，

S△CDE＝HMxE＝（k﹣3+4），

S△BEF＝BFyE＝（﹣3）（），

由S△CDE＝S△BEF，解得：k＝2或，

则：CF的表达式为y＝2x﹣3或y＝x﹣3…③，

将③与二次函数表达式联立，解得：x＝或x＝0（舍去），

故点H为（，﹣）．