题目内容
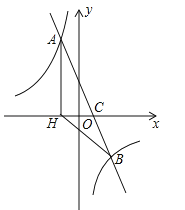
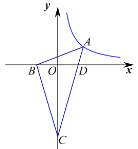
【题目】如图，在
中，
，
，
与
轴交于点
，
，点
在反比例函数
的图象上，且
轴平分
，求
_____．
【答案】
【解析】
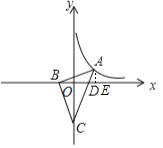
要求k的值，通常可求A的坐标，可作x轴的垂线，构造相似三角形，利用CD=4AD和C（0，-4）可以求出A的纵坐标，再利用三角形相似，设未知数，由相似三角形对应边成比例，列出方程，求出待定未知数，从而确定点A的坐标，进而确定k的值．
解：过A作AE⊥x轴，垂足为E，
∵C（0，-4），
∴OC=4，
∵∠AED=∠COD=90°，∠ADE=∠CDO
∴△ADE∽△CDO，
,
∴AE=1；
又∵y轴平分∠ACB，CO⊥BD，
∴BO=OD，
∵∠ABC=90°，
∴∠OCD=∠DAE=∠ABE=∠BCE，
∵∠DOC=∠ADE=90°
∴△ABE～△COD，
∴
设DE=n，则BO=OD=4n，BE=9n，
∴
，
∴
,
∴OE=5n=,
故点A(，1),
∴k=×1=
故答案为：.
练习册系列答案
相关题目
【题目】超市有
，
两种型号的瓶子，其容量和价格如表，小张买瓶子用来分装15升油（瓶子都装满，且无剩油）；当日促销活动：购买型瓶3个或以上，一次性返还现金5元，设购买型瓶
（个），所需总费用为
（元），则下列说法不一定成立的是（ ）
型号 | A | B |
单个盒子容量（升） | 2 | 3 |
单价（元） | 5 | 6 |
A.购买型瓶的个数是
为正整数时的值B.购买型瓶最多为6个
C.与之间的函数关系式为
D.小张买瓶子的最少费用是28元
