题目内容
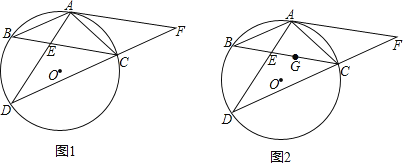
【题目】已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=5![]() .请求出:
.请求出:

(1)∠AOC的度数;
(2)△OAC的面积;
(3)线段AD的长(结果保留根号).
【答案】(1)∠AOC=60°;(2)![]() ;(3)AD=
;(3)AD=![]() .
.
【解析】
(1)根据圆周角定理可得答案;
(2)证明△OAC是等边三角形,可知∠AOH=30°,解直角三角形求出AH即可解决问题;
(3)由切线的性质可得AD⊥OA,然后根据正切的概念求得AD的长.
解:(1)∵∠B=30°,
∴∠AOC=2∠B=60°;
(2)在△AOC中,∵OA=OC,∠AOC=60°,
∴△OAC是等边三角形,
∵OH⊥AC,
∴∠AOH=30°,
∵![]() ,
,
∴AH=OH·tan30°=![]() ,
,
∴AC=2AH=10,
∴![]() ;
;
(3)∵AD是切线,
∴AD⊥OA,
∵△OAC是等边三角形,∠AOC=60°,
∵tan60°=![]() ,OA=AC=10,
,OA=AC=10,
∴AD=OA·tan60°=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】下表是某班体育考试跳绳项目模拟考试时10名同学的测试成绩(单位:个/分钟)
成绩(个/分钟) | 140 | 160 | 169 | 170 | 177 | 180 |
人数 | 1 | 1 | 1 | 2 | 3 | 2 |
则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
A.方差是135B.平均数是170C.中位数是173.5D.众数是177