题目内容
【题目】如图①,抛物线y=﹣x2+bx+c与x轴交于点A和点B(4,0),与y轴交于点C(0,4).
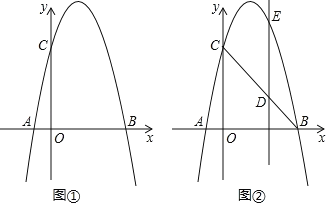
(1)求出抛物线的函数表达式.
(2)抛物线上是否存在一点P,使得S△OBC=4S△AOP,若存在求出点P的坐标;若不存在,请说明理由.
(3)如图②,点D为线段BC上一动点,过点D作DE∥y轴交抛物线于点E,求线段DE长度的最大值.
【答案】(1)y=﹣x2+3x+4;(2)点P坐标(0,4)或(3,4),或(![]() ,﹣4)或(
,﹣4)或(![]() ,﹣4);(3)DE的最大值为4.
,﹣4);(3)DE的最大值为4.
【解析】
(1)利用待定系数法将点B,C代入即可求出抛物线的表达式;
(2)先利用抛物线的表达式求出点A的坐标,进而可求出OA,OB,OC的长度,然后利用面积之间的关系求出点P的纵坐标,再将P的纵坐标代入抛物线的表达式中求出横坐标即可;
(3)先用待定系数法求出直线BC的解析式,然后表示出先对DE的长度,再利用二次函数的性质求最大值即可.
(1)∵抛物线y=﹣x2+bx+c与x轴交于点A和点B(4,0),与y轴交于点C(0,4),
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为:y=﹣x2+3x+4;
(2)∵y=﹣x2+3x+4与x轴交于点A和点B(4,0),
∴0=﹣x2+3x+4,
∴x1=4,x2=﹣1,
∴点A(﹣1,0),且点B(4,0),点C(0,4),
∴AO=1,BO=CO=4,
设点P(x,y)
∵S△OBC=4S△AOP,
∴![]() OB×OC=4
OB×OC=4![]() AO×|y|,
AO×|y|,
∴|y|=4,
∴y=±4,
当y=4时,4=﹣x2+3x+4,
∴x1=0,x2=3,
∴点P坐标(0,4)或(3,4),
当y=﹣4时,﹣4=﹣x2+3x+4,
∴x3![]() ,x4
,x4![]() ,
,
∴点P坐标(![]() ,﹣4)或(
,﹣4)或(![]() ,﹣4),
,﹣4),
综上所述,点P的坐标为(0,4)或(3,4) 或(![]() ,﹣4)或(
,﹣4)或(![]() ,﹣4)
,﹣4)
(3)设直线BC的解析式为![]()
将点B(4,0), C(0,4)代入解析式中得,
![]() 解得
解得![]()
∴直线BC解析式为:y=﹣x+4,
设点E(a,﹣a2+3a+4),则点D(a,﹣a+4),
∴DE=﹣a2+3a+4﹣(﹣a+4)=﹣(a﹣2)2+4,
当a=2时,DE的最大值为4.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数,且
为常数,且![]() )中的
)中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以下结论:
①二次函数![]() 有最小值为
有最小值为![]() ;
;
②当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
③二次函数![]() 的图象与
的图象与![]() 轴只有一个交点;
轴只有一个交点;
④当![]() 时,
时,![]() .
.
其中正确的结论有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()