题目内容
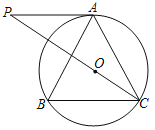
【题目】(1)如图1,点![]() 在
在![]() 上,请在图中用直尺(不含刻度)和圆规作等边三角形
上,请在图中用直尺(不含刻度)和圆规作等边三角形![]() ,使得点
,使得点![]() 、
、![]() 都在
都在![]() 上.
上.
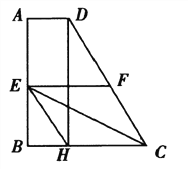
(2)已知矩形![]() 中,
中,![]() ,
,![]() .
.
①如图2,当![]() 时,请在图中用直尺(不含刻度)和圆规作等边三角形
时,请在图中用直尺(不含刻度)和圆规作等边三角形![]() ,使得点
,使得点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上;
上;
②若在该矩形中总能作出符合①中要求的等边三角形![]() ,请直接写出
,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)①见解析;②![]() 的取值范围是
的取值范围是![]() .
.
【解析】
解:(1) 作直径![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作弧,交
为半径作弧,交![]() 于点
于点![]() 、
、![]() ,连
,连![]() 、
、![]() 、
、![]() 即可得到等边三角形
即可得到等边三角形![]() .
.
(2) ①连![]() ,在
,在![]() 上任取一点
上任取一点![]() ,以
,以![]() 为半径作
为半径作![]() ,交
,交![]() 于点
于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作弧,交
为半径作弧,交![]() 于点
于点![]() 、
、![]() ,连
,连![]() 、
、![]() 并延长,交
并延长,交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连
,连![]() ,则
,则![]() 就是所要求作的.
就是所要求作的.
②分两种情况讨论,运用等边三角形的性质和勾股定理得到m的最大值和最小值即可;
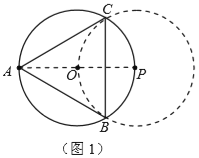
解:(1)如图1,作直径![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作弧,交
为半径作弧,交![]() 于点
于点![]() 、
、![]() ,连
,连![]() 、
、![]() 、
、![]() ,则
,则![]() 就是所要求作的.
就是所要求作的.
(2)①如图2,连![]() ,在
,在![]() 上任取一点
上任取一点![]() ,以
,以![]() 为半径作
为半径作![]() ,交
,交![]() 于点
于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作弧,交
为半径作弧,交![]() 于点
于点![]() 、
、![]() ,连
,连![]() 、
、![]() 并延长,交
并延长,交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连
,连![]() ,则
,则![]() 就是所要求作的.
就是所要求作的.
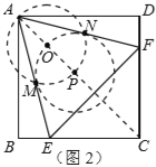
②一开始E点从B点出发,往C的方向运动,AF可以看成AE逆时针旋转60度得到,因此F是往上运动的,但是AE一直在变长,如果BC的长度不变的话,AF就是变少。(但是要保持AE=AF)只能变长BC了。所以E点从B点出发,往C的方向运动过程中,BC一直在变长。F最多只能到D点,因此F在D点处,BC就是最长了,因此得到如下的两个临界值:
如图,当E点与B点重合时,此时是临界点的最小值,
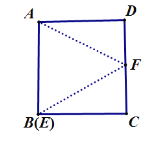
∵△AFE是等边三角形,
∴EF=AB=4,∠AEF=60°,
∴∠FEC=30°,
∴FC=2(直角三角形中30°所对的直角边等于斜边的一半),
∴此时![]() ,
,
当F点与D点重合时,此时是临界点的最大值,
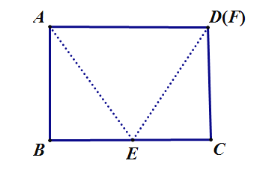
∵△AFE是等边三角形,
∴AD=AE,∠BAE=90°-60°=30°,
假设AD=AE=2x,
∴FC=x(直角三角形中30°所对的直角边等于斜边的一半),
∴此时![]() ,
,
解得![]() ,
,
∴![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案