题目内容
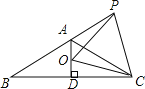
【题目】如图，在△ABC中，AC＝BC，∠ACB＝90°，点D在BC上，BD＝6，CD＝2，点P′是AB上的动点，则PC+PD的最小值是（ ）
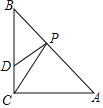
A.7B.8C.9D.10
【答案】D
【解析】
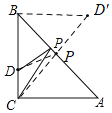
过点B作D'B⊥BC，且BD'＝6，连接CD'交AB于点P，由“SAS”可证△BPD≌△BPD'，可得DP＝D'P，可得PC+PD的最小值为D'C，由勾股定理可求解．
解：如图，过点B作D'B⊥BC，使BD'＝6，连接CD'交AB于点P
∵AC＝BC，∠ACB＝90°，
∴∠ABC＝45°，且BD'⊥BC
∴∠D'BP＝∠DBP＝45°，且BD＝6＝BD'，BP＝BP
∴△BPD≌△BPD'（SAS）
∴DP＝D'P
∴CP+DP＝CP+D'P
∴PC+PD的最小值为D'C，
∵BD＝6，CD＝2
∴BC＝8，
∴D'C＝
∴PC+PD的最小值为10
故选：D．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
