Question

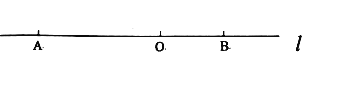
【题目】如图，直线上有两点，， 点是线段上的一点，.若动点，分别从同时出发，向右运动，点的速度为.点的速度为.设运动时间为，当点和点重合时，两点停止运动.

（1）当为何值时，？

（2）当点经过点时，动点从点出发，以的速度也向右运动，当点追上点后立即返回，以的速度向点运动，遇到点后再立即返回，以的速度向点运动，如此往返，当点与点重合时，两点停止运动，此时点也停止运动，在此过程中，点行驶的总路程是多少？

Answer 1

【答案】（1）2s或6.8s（2）20cm

【解析】

（1）先由OA=2OB结合AB=OA+OB=18即可求出OA、OB的长度；分两种情况,由两点间的距离公式结合2OP-OQ=4即可得出关于t的一元一次方程，解之即可得出结论；

（2）点M运动的时间就是点P从点O开始到追到点Q的时间，用这个时间乘以速度即可．

解：（1）∵AB=18cm，OA=2OB，

∴OA+OB=3OB=AB=18cm，

解得：OB=6cm，

OA=2OB=12cm．

12÷3=4秒，当0<t≤4时，如图，

AP=3t，OP=12-3t，BQ=t，OQ=6+t，

∵2OP-OQ=4，

∴2(12-3t)-(6+t)=4，

解得

t=2；

当点P与点Q重合时，

3t=18+t，

t=9，

当4＜t≤9时，如图，

OP=3t-12，OQ=6+t，

则2(3t-12)-(6+t)=4，

解得t=6.8．

故当t为2s或6.8s时，2OP-OQ=4；

（2）4×（9-4）=20（cm）．

答：在此过程中，点M行驶的总路程是20cm．