题目内容
【题目】在![]() ,
,![]() 中,
中,![]() ,连接
,连接![]() ,
,![]() 是
是![]() 中点,连接
中点,连接![]()
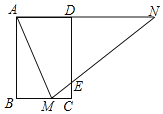
(1)如图1,若![]() 三点在同一直线上,
三点在同一直线上,![]() ,已知
,已知![]() ,求线段
,求线段![]() 的长;
的长;
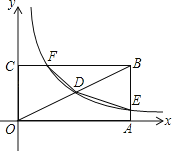
(2)如图2,若![]() ,求证:
,求证:![]() 为等腰直角三角形;
为等腰直角三角形;
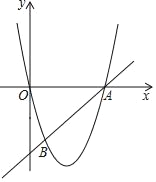
(3)如图3,若![]() ,请判断
,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
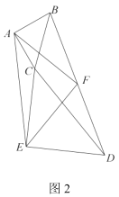
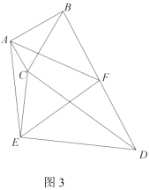
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 为等边三角形,理由见解析
为等边三角形,理由见解析
【解析】
(1)连接CF,利用等腰三角形的性质,可证得AB=AC, ED=CE,利用直角三角形的性质,易证CF=BF,再根据SSS证明△ACF≌△ABF,利用全等三角形的性质,就可求出∠CAF的度数,同理可得到∠CEF的度数,由此可得到△AEF是等腰直角三角形,可求出AC,CE的长,然后求出AF的长.(2)取BC中点M,CD中点N,连接AM,MF,EN,FN,易证FM为△BCD的一条中位线利用中位线定理可得到FM∥CD,FM=CN,利用有一组对边平行且相等的四边形是平行四边形,可知四边形MCNF为平行四边形,再利用SAS证明△AMF≌△FNE,利用全等三角形的性质,可证得AF=EF,∠1=∠3,然后证明∠AFE=90°,继而可证得结论.(3)取BC中点M,CD中点N,连接AM,MF,EN,FN,同理可证四边形MCNF为平行四边形,利用平行四边形的性质,可证得CM=FN, MF=CN, ∠CMF=∠FNC,再结合已知条件可证得AM=FN,∠AMF=∠FNE,然后利用全等三角形的判定和性质,可证得AF=EF,∠1=∠3,再求出∠AFE=60°,即可判断△AEF的形状.
(1)连接![]() ,
,

![]() 在
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() 三点在同一直线上,
三点在同一直线上,
![]() ,
,
![]() 为
为![]() 中点,
中点,
![]() ,
,
![]() 在
在![]() 和
和![]() 中,
中,
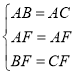 ,
,
![]() ,
,
![]() ,
,
同理:![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,
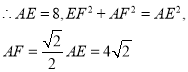
(2)证明:取![]() 中点
中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
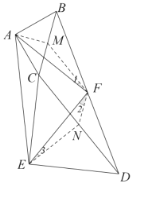
![]() 为
为![]() 中点,
中点,
![]() 为
为![]() 的一条中位线,
的一条中位线,
![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
![]() 在
在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,
![]() ,
,
同理:![]() ,
,
![]() ,
,
![]() ,
,
![]() 和
和![]() 中,
中,
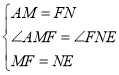 ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
(3)证明:取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
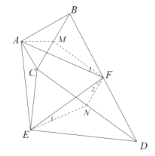
![]() 为
为![]() 中点,
中点,
![]() 为
为![]() 的一条中位线,
的一条中位线,
![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
![]() 在
在![]() 中,
中,![]() 为
为![]() 的中点,∠ABC=30°
的中点,∠ABC=30°
![]() ,
,
同理:![]() ,
,
![]() ,
,![]() ,
,
![]() 和
和![]() 中,
中,
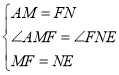 ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 为等边三角形.
为等边三角形.

【题目】如图,AB为![]() 的直径,BC为
的直径,BC为![]() 的切线,弦AD∥OC,直线CD交的BA延长线于点E,连接BD.下列结论:①CD是
的切线,弦AD∥OC,直线CD交的BA延长线于点E,连接BD.下列结论:①CD是![]() 的切线;②
的切线;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论的个数有( )
.其中正确结论的个数有( )
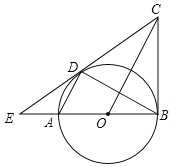
A. 4个B. 3个C. 2个D. 1个
【题目】据第四次全国经济普查的数据表明,中国经济已经开始由高速增长转向高质量发展,供给侧结构性改革初见成效.各地产品质量监管部门也严抓质量,整顿生产,促进经济更好发展.某质量监管部门对甲、乙两家工厂生产的同种产品进行检测,分别随机抽取50件产品,并对产品的某项关键质量指标做检测,获得质量指标检测值![]() ,对数据整理分析的部分信息如下:
,对数据整理分析的部分信息如下:
(1)甲、乙两工厂的样本数据频数分布表如下:
工厂 | 类别 |
|
|
|
|
| 合计 |
甲工厂 | 频数 | 0 |
| 10 | 3 | 50 | |
频率 | 0.00 | 0.24 |
| 0.06 | 1.00 | ||
乙工厂 | 频数 | 3 | 15 | 13 | 18 | span>1 | 50 |
频率 | 0.06 | 0.30 | 0.26 | 0.36 | 0.02 | 1.00 |
其中,乙工厂样品质量指标检测值在![]() 范围内的数据分别是:
范围内的数据分别是:
100, 98, 98, 99, 102, 97, 95, 101, 98, 100, 98, 102, 104
(2)两工厂样本数据的部分统计数据如下:
平均数 | 中位数 | 众数 | 方差 | |
甲工厂 | 97.3 | 99.5 | 96 | 78.3 |
乙工厂 | 97.3 |
| 107 | 135.4 |
根据以上信息,回答下列问题:
(1)表格中,![]() ,
,![]() ,
,![]() ;
;
(2)已知质量指标检测值在![]() 内,属于合格产品.若乙工厂某批次产品共1万件,估计该批产品中不合格的有多少件?
内,属于合格产品.若乙工厂某批次产品共1万件,估计该批产品中不合格的有多少件?
(3)若质量指标检测值为100时为优秀,偏离100越小,产品质量越高.现有一家公司需大量采购该种产品,根据题目给定的数据,你认为选择哪家工厂的产品更好?请说明理由.