题目内容
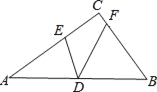
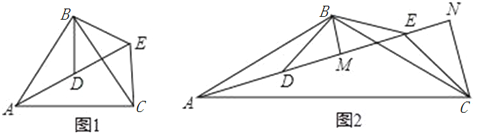
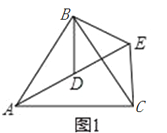
【题目】如图,△ABC和△DBE均为等腰三角形,点A,D,E在同一直线上,连接CE.
(1)如图1,若∠BAC=∠BCA=∠BDE=∠BED=55°
①求证:AD=CE;
②求∠AEC的度数.
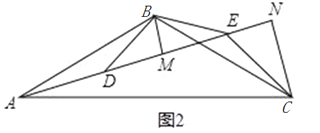
(2)如图2,若∠ABC=∠DBE=120°,BM为△BDE中DE边上的高,CN为△ACE中AE边上的高,![]() 试证明:AE=
试证明:AE=![]() .
.
【答案】(1)①证明见解析②70°(2)![]()
【解析】(1)关键全等三角形的判定方法,判断出△BAD≌△CAE,即可判断出BD=CE.
(2)①首先根据△ACB和△CE均为等腰三角形,可得AC=BC,CD=CE,∠ACB=∠DCE=90°,据此判断出∠ACD=∠BCE;然后根据全等三角形的判定方法,判断出△ACD≌△BCE,即可判断出BE=AD,∠BEC=∠ADC,进而判断出∠AEB的度数为90°即可;
解:(1)证明:∵∠ABD+∠DBC=∠CBE+∠DBC=55°,
∴∠ABD=∠CBE.
∵△ABC和△DBE均为以点B为腰上顶点的等腰三角形.
∴BA=BC,BD=BE
∴△ABD≌△CBE.
∴AD=CE
②:解:∵△ABD≌△CBE(已证)
∴∠BDA=∠BEC=180°-∠BDE
∵∠AEC=∠BEC-∠BED
∴∠AEC =180°-2∠BDE=70°
(2)同理可证:AD=CE,∠AEC=120° ,∴∠CEN=60°,
∵CN为△ACE中AE边上的高,
∴∠ECN=30°,∵CN=a,![]()
根据勾股定理:CE=![]() ,
,
∴AD=CE=![]() ,
,![]()
∵△DBE为等腰三角形, BM为△BDE中DE边上的高
∴DE=2DM,
∵∠DBE=120°,∴∠BDM=30°,
∴根据勾股定理:DM=![]() ,
,![]()
∴DE=2DM=2![]()
![]() ,
,
∴AE=AD+DE=![]() +2
+2![]()
![]()
“点睛”此题主要考查了全等三角形的判定方法和性质,等腰直角三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:在判定三角形全等时,关键是选择恰当的判定条件.