题目内容
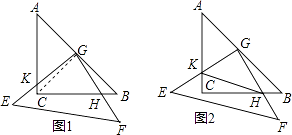
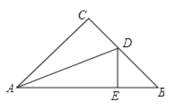
【题目】数学兴趣小组在活动时，老师提出了这样一个问题：如图1，在△ABC中，AB=8，AC=6，D是BC的中点，求BC边上的中线AD的取值范围．
小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE=AD，再证明“△ADC≌△EDB”．
（1）探究得出AD的取值范围是_____；
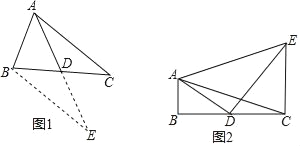
（2）（问题解决）如图2，△ABC中，∠B=90°，AB=2，AD是△ABC的中线，CE⊥BC，CE=4，且∠ADE=90°，求AE的长．
【答案】（1）1＜AD＜7；（2）AE=6
【解析】
（1）根据全等三角形的性质、三角形的三边关系计算；
（2）延长AD交EC的延长线于F，证明△ABD≌△FCD，根据全等三角形的性质解答．
（1）∵△ADC≌△EDB，
∴BE=AC=6，
8-6＜AE＜8+6，
∴1＜AD＜7，
故答案为：1＜AD＜7；
（2）延长AD交EC的延长线于F，
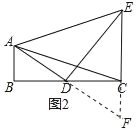
∵AB⊥BC，EF⊥BC，
∴∠ABD=∠FCD，
在△ABD和△FCD中，
，
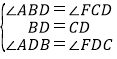∴△ABD≌△FCD，
∴CF=AB=2，AD=DF，∵∠ADE=90°，∴AE=EF，
∵EF=CE+CF=CE+AB=4+2=6，
∴AE=6.
练习册系列答案
相关题目
