题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 上一动点,
上一动点,![]() 点从
点从![]() 点以1个单位/秒的速度向
点以1个单位/秒的速度向![]() 点运动,远动到
点运动,远动到![]() 点即停止,经过
点即停止,经过![]() 点作
点作![]() ,交
,交![]() 于点
于点![]() ,以
,以![]() 为一边在
为一边在![]() 一侧作正方形
一侧作正方形![]() ,在
,在![]() 点运动过程中,设正方形
点运动过程中,设正方形![]() 与
与![]() 的重叠面积为
的重叠面积为![]() ,运动时间为
,运动时间为![]() 秒,如图2是
秒,如图2是![]() 与
与![]() 的函数图象.
的函数图象.
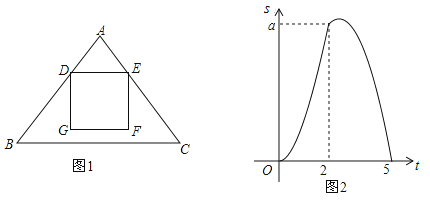
(1)求![]() 的长;
的长;
(2)求![]() 的值;
的值;
(3)求![]() 与
与![]() 的函数关系式.
的函数关系式.
【答案】(1)![]() (2)
(2)![]()
(3)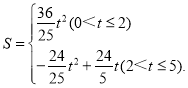
【解析】
(1)根据图中信息得到t=2时,正方形DEFG的边FG在BC边上,设DE=4x,在△BDG中表示出DG,BG利用勾股定理解决即可.
(2)a的值就是图1中的正方形面积.
(3)分两种情形①0<t≤2,②2<t≤5求出重叠部分面积即可.
解:(1)由题意t=2时,正方形DEFG在如图位置,
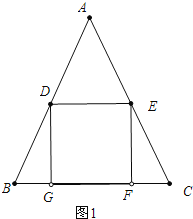
此时AD=2,BD=3,
设DE=4x,
∵DE∥BC,
![]()
∴![]()
∴ ![]() ∴
∴![]()
根据等腰三角形的对称性可知:BG=FC=3x,
在RT△BDG中,∵![]()
∴![]()
∵x>0, ∴![]()
∴BC=10x=6,
(2)由图1可知t=2时,a的值就是图1中的正方形面积,
即![]()
(3)在图2中,作AH⊥BC于H,交DE于K,
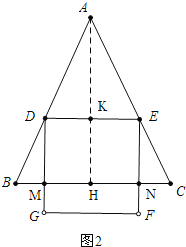
由(1)可知AH![]()
∵DK∥BH,
![]()
∴ ![]()
![]()
∴![]()
∴![]() DE=2DK=
DE=2DK=![]()
当0<t≤2时,![]()
当2<t≤5时,∵DM∥AH,
![]() ,
,
∴ ![]()
∴![]()
∴![]()
∴![]()
综上所述: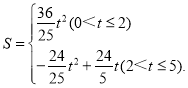 .
.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目