题目内容
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠OAC=4.

(1)求抛物线的解析式:
(2)若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值.
【答案】(1)y=x2﹣3x﹣4;(2)△MPH的周长的最大值为![]() .
.
【解析】
(1)先由锐角三角函数的定义求得C的坐标,从而得到点B的坐标,设抛物线的解析式为y=a(x+1)(x-4),将点C的坐标代入求解即可;
(2)先求得抛物线的对称轴,从而得到点D(3,-4),然后可求得直线AD的解析式y=-x-1,故∠BAD=45°,接下来证明△PMD为等腰直角三角形,所当PM有最大值时三角形的周长最大,设P(a,a2-3a-4),M(-a-1),则PM=-a2+2a+3,然后利用配方可求得PM的最大值,最后根据△MPH的周长=![]() 求解即可.
求解即可.
(1)∵点A的坐标为(﹣1,0),
∴OA=1.
又∵tan∠OAC=4,
∴OC=4,
∴C(0,﹣4).
∵OC=OB,
∴OB=4,
∴B(4,0).
设抛物线的解析式为y=a(x+1)(x﹣4),
∵将x=0,y=﹣4代入得:﹣4a=﹣4,解得a=1,
∴抛物线的解析式为y=x2﹣3x﹣4.
(2)∵抛物线的对称轴为![]() ,C(0,﹣4),
,C(0,﹣4),
∵点D和点C关于抛物线的对称轴对称,
∴D(3,﹣4),
设直线AD的解析式为y=kx+b.
∵将A(﹣1,0)、D(3,﹣4)代入得 ![]() ,
,
解得k=﹣1,b=﹣1,
∴直线AD的解析式y=﹣x﹣1.
∵直线AD的一次项系数k=﹣1,
∴∠BAD=45°.
∵PM平行于y轴,
∴∠AEP=90°,
∴∠PMH=∠AME=45°.
∴△MPH的周长=![]() ,
,
设P(a,a2﹣3a﹣4),则M(a,﹣a﹣1),
则PM═﹣a﹣1﹣(a2﹣3a﹣4)=﹣a2+2a+3=﹣(a﹣1)2+4.
∴当a=1时,PM有最大值,最大值为4.
∴△MPH的周长的最大值=![]() .
.

【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
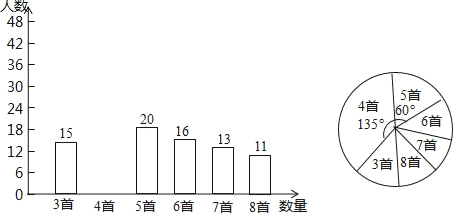
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.