题目内容
【题目】如图,AD为△ABC中∠ BAC的外角平分线,BD⊥AD于D,E为BC中点,DE=5,AC=3,则AB长为()

A.8.5B.8C.7.5D.7
【答案】D
【解析】
延长BD、CA交于点F,易证△ADF![]() △ADB(ASA),则BD=DF,AB=AF,得到点D为BF中点,即DE为△BCF的中位线,再根据已知线段的长度,即可顺利求得AB的长.
△ADB(ASA),则BD=DF,AB=AF,得到点D为BF中点,即DE为△BCF的中位线,再根据已知线段的长度,即可顺利求得AB的长.
解:如图,分别延长BD、AC交于点F,
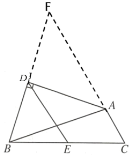
∵AD为△ABC中∠BAC的外角平分线,
∴∠FAD=∠BAD,
∵BD⊥AD,
∴∠FDA=∠BDA=90°,
在△BDA和△FDA中,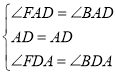 ,
,
∴△BDA![]() △FDA(ASA),
△FDA(ASA),
∴AB=AF,BD=FD,即D为BF的中点,
∵E为BC中点,
∴DE为△BCF的中位线,
∵DE=5,AC=3,
∴CF=2DE=2![]() 5=10,
5=10,
∴AF=CF-AC=10-3=7.
∴AB=AF=7.
故选D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





