题目内容
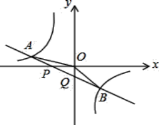
【题目】如图,已知直线y=k1x+b与x轴、y轴相交于P,Q两点,与y=![]() 的图象相交于A(-2,m),B(1,n)两点,连接OA,OB,给出下列论:①k1k2<0;②m+
的图象相交于A(-2,m),B(1,n)两点,连接OA,OB,给出下列论:①k1k2<0;②m+![]() n=0;③S△AOP=S△BOQ;④不等式k1x+b>
n=0;③S△AOP=S△BOQ;④不等式k1x+b>![]() 的解集为x<-2或0<x<1.其中正确的结论是________.
的解集为x<-2或0<x<1.其中正确的结论是________.
【答案】②③④
【解析】
根据一次函数和反比例函数的性质得到k1k2>0,故①错误;把A(-2,m)、B(1,n)代入y=![]() 中得到-2m=n故②正确;把A(-2,m)、B(1,n)代入y=k1x+b得到y=-mx-m,求得P(-1,0),Q(0,-m),根据三角形的面积公式即可得到S△AOP=S△BOQ;故③正确;根据图象得到不等式k1x+b>
中得到-2m=n故②正确;把A(-2,m)、B(1,n)代入y=k1x+b得到y=-mx-m,求得P(-1,0),Q(0,-m),根据三角形的面积公式即可得到S△AOP=S△BOQ;故③正确;根据图象得到不等式k1x+b>![]() 的解集是x<-2或0<x<1,故④正确.
的解集是x<-2或0<x<1,故④正确.
:由图象知,k1<0,k2<0,
∴k1k2>0,故①错误;
把A(-2,m)、B(1,n)代入y=![]() 中得-2m=n,
中得-2m=n,
∴m+![]() n=0,故②正确;
n=0,故②正确;
把A(-2,m)、B(1,n)代入y=k1x+b得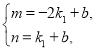
∴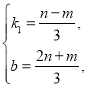 ,
,
∵-2m=n,
∴y=-mx-m,
∵已知直线y=k1x+b与x轴、y轴相交于P、Q两点,
∴P(-1,0),Q(0,-m),
∴OP=1,OQ=m,
∴S△AOP=![]() m,S△BOQ=
m,S△BOQ=![]() m,
m,
∴S△AOP=S△BOQ;故③正确;
由图象知不等式k1x+b>![]() 的解集是x<-2或0<x<1,故④正确;
的解集是x<-2或0<x<1,故④正确;
故答案为:②③④.

练习册系列答案
相关题目