题目内容
【题目】如图1，在平面直角坐标系中，点A（0，4），点B（m，0），以AB为边在右侧作正方形ABCD．
（1）当点B在x轴正半轴上运动时，求点C点的坐标．（用m表示）
（2）当m=0时，如图2，P为OA上一点，过点P作PM⊥PC，PM=PC，连MC交OD于点N，求AM+2DN的值；
（3）如图3，在第（2）问的条件下，E、F分别为CD、CO上的点，作EG∥x轴交AO于G，作FH∥y轴交AD于H，K是EG与FH的交点．若S四边形KFCE=2S四边形AGKH，试确定∠EAF的大小，并证明你的结论．
【答案】（1）C(m+4，m)；（2）AM+2DN=4
；（3）∠EAF=45°，证明见解析
【解析】
（1）如图1中，作
轴于
．利用全等三角形的性质即可解决问题；
（2）如图2中，作
轴于，作
交
于
．构造平行四边形，全等三角形解决问题即可；
（3）如图3中，延长
到
，使得
．则
．设
，
，由题意
，
，
，
，利用勾股定理想办法证明
，再证明
，可得
即可解决问题；
解：（1）如图1中，作轴于．
，
，
，
，
又
，
，
，
，
．
（2）如图2中，作轴于，作交于．
，
，
，
，
，
，
，
，
，
，
，
，
，
，
四边形
是平行四边形，
，
，
，
，
，
，
，
．
（3）如图3中，延长到，使得．则
．
设，，由题意，，，，
，
，
，
，
，
在
中，
，
，
，
，
，
，
，
，
．
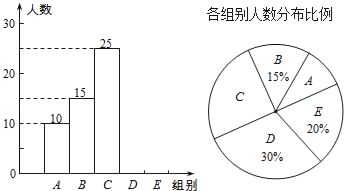
【题目】某校举行全体学生“汉字听写”比赛，每位学生听写汉字39个．随机抽取了部分学生的听写结果，绘制成如下的图表．
组别 | 正确字数x | 人数 |
A | 0≤x＜8 | 10 |
B | 8≤x＜16 | 15 |
C | 16≤x＜24 | 25 |
D | 24≤x＜32 | m |
E | 32≤x＜40 | n |
根据以上信息完成下列问题：
（1）统计表中的m＝ ，n＝ ，并补全条形统计图；
（2）扇形统计图中“C组”所对应的圆心角的度数是 ；
（3）已知该校共有900名学生，如果听写正确的字的个数少于24个定为不合格，请你估计该校本次听写比赛不合格的学生人数．
【题目】某学校计划租用6辆客车送一批师生参加一年一度的哈尔滨冰雕节，感受冰雕艺术的魅力．现有甲、乙两种客车，它们的载客量和租金如下表．设租用甲种客车x辆，租车总费用为y元．
甲种客车 | 乙种客车 | |
载客量（人/辆） | 45 | 30 |
租金（元/辆） | 280 | 200 |
（1）求出y（元）与x（辆）之间的函数关系式，指出自变量的取值范围；
（2）若该校共有240名师生前往参加，领队老师从学校预支租车费用1650元，试问预支的租车费用是否可以结余？若有结余，最多可结余多少元？
