题目内容
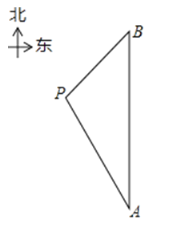
【题目】如图所示,在Rt△ABC中,斜边AC的中点M关于BC的对称点为点O,将△ABC绕点O顺时针旋转至△DCE,连接BD,BE,
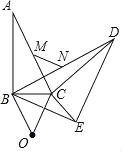
(1)在①∠BOE,②∠ACD,③∠COE中,等于旋转角的是 (填写序号即可);
(2)判断∠A和∠BEC的数量关系,并证明;
(3)点N是BD的中点,连接MN,若MN=2,求BE的值.
【答案】(1)③;
(2)∠A=∠BEC,理由见解析;
(3)BE=4.
【解析】
(1)根据旋转的性质即可得出结论;
(2)先判断出MA=MB=MC=![]() AC,进而得出∠A=∠ABM=α,即:∠BMC=∠A+∠ABM=2α,再判断出∠BOC=∠BMC=2α,判断出点C,B,E在以O为圆心,OB为半径的圆上,即可得出结论;
AC,进而得出∠A=∠ABM=α,即:∠BMC=∠A+∠ABM=2α,再判断出∠BOC=∠BMC=2α,判断出点C,B,E在以O为圆心,OB为半径的圆上,即可得出结论;
(3)先判断出∠DEC=∠ACB=90°-α,再判断出∠MBC=∠ACB=90°-α,进而判断出∠MBE+∠BED=180°,得出BF∥DE,即可判断出四边形BFDE是平行四边形,即可得出结论.
解:(1)如图1,连接OA,OD,OE,
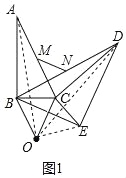
由旋转知,旋转角为∠BOC=∠AOD=∠COE,
故答案为③;
(2)∠A=∠BEC,
理由如下:
如图2,连接BM,OE,
设∠A=α,
在Rt△ABC中,点M是AC中点,
∴MA=MB=MC=![]() AC,
AC,
∴∠A=∠ABM=α,
∴∠BMC=∠A+∠ABM=2α,
∵点M和点O关于直线BC对称,
∴∠BOC=∠BMC=2α,
∵OC=OB=OE,
∴点C,B,E在以O为圆心,OB为半径的圆上,
∴∠BEC=![]() ∠BOC=α
∠BOC=α
∴∠A=∠BEC;
(3)如图3,连接BM并延长至点F,使BM=MF,连接FD,

∵∠A=α,∠ABC=90°,
∴∠ACB=90°﹣∠A=90°﹣α,
∴∠DEC=∠ACB=90°﹣α,
由(2)知,∠BEC=α,
∴∠BED=∠BEC+∠DEC=90°,
∵BC=CE,
∴∠CBE=∠CEB=α,
∵MB=MC,
∴∠MBC=∠ACB=90°﹣α,
∴∠MBE=∠MBC+∠CBE=90°,
∴∠MBE+∠BED=180°,
∴BF∥DE,
∵BF=2BM,AC=2BM,
∴BF=AC,
∵AC=DE,
∴BF=DE,
∴四边形BFDE是平行四边形,
∴DF=BE,
∵BM=MF,BN=ND,
∴MN=![]() DF,
DF,
∴MN=![]() BE,
BE,
∴BE=2MN=4.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案