题目内容
【题目】我们知道,经过原点的抛物线解析式可以是![]() 。
。
(1)对于这样的抛物线:
当顶点坐标为(1,1)时,a= ;
当顶点坐标为(m,m),m≠0时,a 与m之间的关系式是 ;
(2)继续探究,如果b≠0,且过原点的抛物线顶点在直线![]() 上,请用含k的代数式表示b;
上,请用含k的代数式表示b;
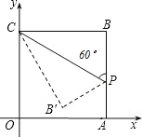
(3)现有一组过原点的抛物线,顶点A1,A2,…,An在直线![]() 上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
【答案】(1)-1;![]() (2)
(2)![]() (3)3,6,9
(3)3,6,9
【解析】
解:(1)-1;![]() 。
。
(2)∵过原点的抛物线顶点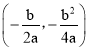 在直线
在直线![]() 上,∴
上,∴![]() 。
。
∵b≠0,∴![]() 。
。
(3)由(2)知,顶点在直线![]() 上,横坐标依次为1,2,…,n(n为正整数,且n≤12)的抛物线为:
上,横坐标依次为1,2,…,n(n为正整数,且n≤12)的抛物线为:![]() ,即
,即![]() 。
。
对于顶点在在直线![]() 上的一点Am(m,m)(m为正整数,且m≤n),依题意,作的正方形AmBmCmDm边长为m,点Dm坐标为(2 m,m),
上的一点Am(m,m)(m为正整数,且m≤n),依题意,作的正方形AmBmCmDm边长为m,点Dm坐标为(2 m,m),
若点Dm在某一抛物线![]() 上,则
上,则
![]() ,化简,得
,化简,得![]() 。
。
∵m,n为正整数,且m≤n≤12,∴n=4,8,12,m=3,6,9。
∴所有满足条件的正方形边长为3,6,9。
(1)当顶点坐标为(1,1)时,由抛物线顶点坐标公式,有 ,即
,即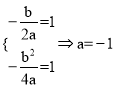 。
。
当顶点坐标为(m,m),m≠0时,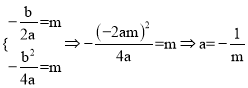 。
。
(2)根据点在直线上,点的坐标满足方程的关系,将抛物线顶点坐标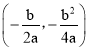 代入
代入![]() ,
,
化简即可用含k的代数式表示b。
由于抛物线与直线只有一个公共点,意味着联立解析式后得到的一元二次方程,其根的判别式等于0,由此可求出m的值和D点坐标。
(3)将依题意,作的正方形AmBmCmDm边长为m,点Dm坐标为(2 m,m),将(2 m,m)代入抛物线![]() 求出m,n的关系,即可求解。
求出m,n的关系,即可求解。

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案