题目内容
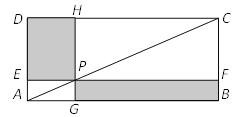
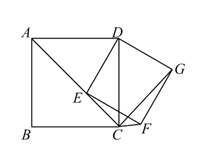
【题目】如图,已知四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG。
(1)求证:矩形DEFG是正方形。
(2)当点E从A点运动到C点时;
①求证:∠DCG的大小始终不变;
②若正方形ABCD的边长为2,则点G运动的路径长为 。
【答案】(1)详见解析;(2)①详见解析;②![]()
【解析】
(1)要证明矩形DEFG为正方形,只需要证明它有一组临边(DE和EF)相等即可,而要证明两条线段相等,需证明它们所在的三角形全等,如下图本小题的关键是证明△EMF≌△END,∠MEF=∠NED可用等角的余角证明,EM=EN可用角平分线上的点到角两边距离相等,∠EMF和∠END为一组直角相等,所以可以用ASA证明它们全等;
(2)此类题,前面的问题是给后面做铺垫,第一问已经证明四边形DEFG为正方形,结合第一问我们很容易发现并证明△ADE≌△CDG,从而得到∠DCG=∠CAD=45°;
(3)当当E点在A处时,点G在C处;当E点在C处时,点G在AD的延长线上,并且AD=DG,以CD为边作正方形,我们会发现G点的运动轨迹刚好是正方形的对角线,它的长度等于![]() .
.
证明:(1)
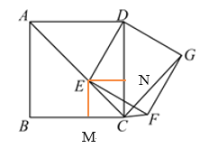
作EM⊥BC,EN⊥CD,
∵四边形ABCD为正方形
∴∠DCB=90°,∠ACB=∠ACD=45°
又∵EM⊥BC,EN⊥CD,
∴EM=EN(角平分线上的点到角两边距离相等),
∠MEN=90°,
∴∠MEF+∠NEF=90°,
∵四边形DEFG为矩形,
∴∠DEF=90°,
∴∠NED+∠NEF=90°,
∴∠MEF=∠NED,
在△EMF和△END中
∵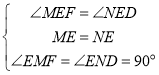
∴△EMF≌△END,
∴DE=DF,
∴矩形DEFG为正方形;
(2)①证明:∵正方形ABCD、DEFG
∴AD=CD,ED=GD
∵∠ADE+∠DEC=90°,∠CDG+∠EDC=90°
∴∠ADE=∠CDG
在△ADE和△CDG中,
∵AD=CD,∠ADE=∠CDG,ED=GD
∴△ADE≌△CDG
∴∠DCG=∠EAD=45°
∴∠DCG的大小始终保持不变
②
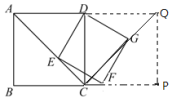
以CD为边作正方形DCPQ,连接QC
∴∠DCQ=45°,
又∵∠DCG=45°
∴C、G、Q在同一条直线上,
当E点在A处时,点G在C处;当E点在C处时,点G在Q处,
∴G点的运动轨迹为QC,
∵正方形ABCD的边长为2
所以QC=![]() ,
,
即点G运动的路径长为![]()