题目内容
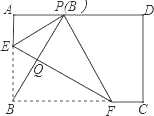
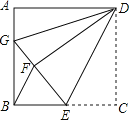
【题目】如图，正方形ABCD中，
，点E在边BC上，
，将
沿DE对折至
，延长EF交边AB于点C，连接DG，BF，给出以下结论：
≌
；
；
；
∽
，其中所有正确结论的个数是
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】分析：根据正方形的性质和折叠的性质可得AD=DF，∠A=∠GFD=90°，于是根据“HL”判定Rt△ADG≌Rt△FDG，再由GF+GB=GA+GB=12，EB=EF，△BGE为直角三角形，可通过勾股定理列方程求出AG=4，BG=8，EG=10，再抓住△BEF是等腰三角形，而△GED显然不是等腰三角形，判断④的正确性．
详解：由折叠可知，DF=DC=DA，∠DFE=∠C=90°， ∴∠DFG=∠A=90°，
在Rt△ADG和Rt△FDG中，AD=DF，DG=DG， ∴Rt△ADG≌Rt△FDG，故①正确；
∵正方形边长是12， ∴BE=EC=EF=6， 设AG=FG=x，则EG=x+6，BG=12-x，
由勾股定理得：
， 解得：x=4，
∴AG=GF=4，BG=8，EG=10， BG=2AG，故②、③正确；
BE=EF=6，△BEF是等腰三角形，易知△GED不是等腰三角形，故④错误；则选C．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
