题目内容
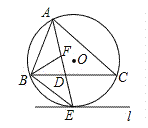
【题目】 如图,AB为⊙O的弦,C为劣弧AB的中点.
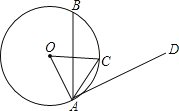
(1)若⊙O的半径为5,AB=8,求tan∠BAC;
(2)若∠DAC=∠BAC,且点D在⊙O的外部,判断AD与⊙O的位置关系,并说明理由.
【答案】(1)![]() ;(2)AD与⊙O相切
;(2)AD与⊙O相切
【解析】
试题分析:(1)根据垂径定理得到直角三角形,分别求出要求正切值的角的对边与邻边,就可以求其正切值;
(2)证明直线与圆相切可以转化为证明直线垂直经过切点的半径.
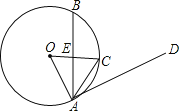
解:(1)如图,∵AB为⊙O的弦,C为劣弧AB的中点,AB=8,
∴OC⊥AB于E,
∴![]() ,
,
又∵AO=5,
∴![]() ,
,
∴CE=OC﹣OE=2,
在Rt△AEC中,![]() ;
;
(2)AD与⊙O相切.理由如下:
∵OA=OC,
∴∠C=∠OAC,
∵由(1)知OC⊥AB,
∴∠C+∠BAC=90°.
又∵∠BAC=∠DAC,
∴∠OAC+∠DAC=90°,
∴AD与⊙O相切.

 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案【题目】根据北京市统计局的2013-2016年空气质量的相关数据,绘制统计图如下:
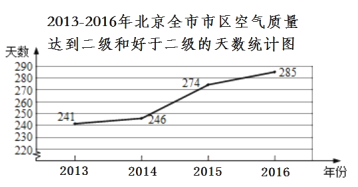
(1)由统计图中的信息可知道,北京全年市区空气质量达到二级和好于二级的天数与上一年相比,增加最多的是 年,增加了 天;
(2)表1是根据《中国环境发展报告(2017)》公布的数据绘制的2016年十个城市空气质量达到二级和好于二级的天数点全年天数百分比的统计表,请将表1中的空缺部分补充完整(精确到1%).
(表1)2016年十个城市空气质量达到二级和好于二级的天数占全年天数百分比统计表
城市 | 北京 | 上海 | 天津 | 昆明 | 杭州 | 广州 | 南京 | 成都 | 沈阳 | 西宁 |
百分比(%) | 91 | 84 | 100 | 89 | 96 | 86 | 86 | 90 | 77 |
(3)根据表1中的数据将十个城市划分为三个组,百分比不低于95%的为![]() 组,不低于85%且低于95%的为
组,不低于85%且低于95%的为![]() 组,低于85%的为
组,低于85%的为![]() 组,按此标准,
组,按此标准,![]() 组城市数量在这十个城市中所占的百分比为 ;请你补全扇形统计图.
组城市数量在这十个城市中所占的百分比为 ;请你补全扇形统计图.