题目内容
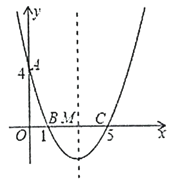
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 两点,其对称轴与
两点,其对称轴与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)连接![]() ,在直线
,在直线![]() 的下方的抛物线上,是否存在一点
的下方的抛物线上,是否存在一点![]() ,使
,使![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ;(2)
;(2)![]() 点坐标为
点坐标为![]() .理由见解析;(3)在直线
.理由见解析;(3)在直线![]() 的下方的抛物线上存在点
的下方的抛物线上存在点![]() ,使
,使![]() 面积最大.点
面积最大.点![]() 的坐标为
的坐标为![]() .
.
【解析】
(1)根据点B,C的坐标,利用待定系数法可求出抛物线的解析式,再利用二次函数的性质可求出抛物线的对称轴;
(2)连接![]() 交对称轴于点
交对称轴于点![]() ,此时
,此时![]() 的周长最小,利用二次函数图象上点的坐标特征可求出点
的周长最小,利用二次函数图象上点的坐标特征可求出点![]() 的坐标,由点
的坐标,由点![]() ,B的坐标,利用待定系数法可求出直线AC的解析式,再利用一次函数图象上点的坐标特征可求出点P的坐标;
,B的坐标,利用待定系数法可求出直线AC的解析式,再利用一次函数图象上点的坐标特征可求出点P的坐标;
(3)过点N作NE∥y轴交AC于点E,交x轴于点F,过点A作AD⊥NE于点D,设点N的坐标为(t,![]() t2-
t2-![]() t+4)(0<t<5),则点E的坐标为(t,-
t+4)(0<t<5),则点E的坐标为(t,-![]() t+4),进而可得出NE的长,由三角形的面积公式结合S△CAN=S△NAE+S△NCE可得出S△CAN关于t的函数关系式,再利用二次函数的性质即可解决最值问题.
t+4),进而可得出NE的长,由三角形的面积公式结合S△CAN=S△NAE+S△NCE可得出S△CAN关于t的函数关系式,再利用二次函数的性质即可解决最值问题.
(1)根据已知条件可设抛物线的解析式为![]() ,
,
∴![]() ,
,
∴抛物线的对称轴是![]() ;
;
(2)![]() 点坐标为
点坐标为![]() .
.
理由如下:
∵点![]() (0,4),抛物线的对称轴是
(0,4),抛物线的对称轴是![]() ,
,
∴点![]() 关于对称轴的对称点
关于对称轴的对称点![]() 的坐标为(6,4),
的坐标为(6,4),
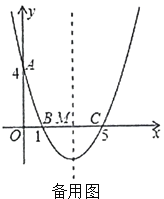
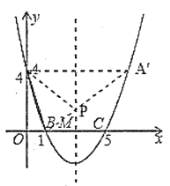
如图1,连接![]() 交对称轴于点
交对称轴于点![]() ,连接
,连接![]() ,此时
,此时![]() 的周长最小.
的周长最小.
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() (6,4),
(6,4),![]() (1,0)代入得
(1,0)代入得![]() ,
,
解得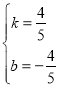 ,
,
∴![]() ,
,
∵点![]() 的横坐标为3,
的横坐标为3,
∴点![]() 的纵坐标为
的纵坐标为![]() ,
,
∴所求点![]() 的坐标为
的坐标为![]() .
.
(3)在直线![]() 的下方的抛物线上存在点
的下方的抛物线上存在点![]() ,使
,使![]() 面积最大.
面积最大.
设![]() 点的横坐标为
点的横坐标为![]() ,此时点
,此时点![]() ,
,
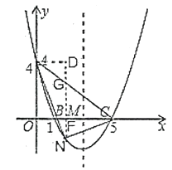
如图2,过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() ;作
;作![]() 于点
于点![]() ,
,
由点![]() (0,4)和点
(0,4)和点![]() (5,0)得直线
(5,0)得直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入得
代入得![]() ,则
,则![]() ,
,
此时![]() ,
,
∵![]() ,
,
∴![]()
![]() ,
,
∴当![]() 时,
时,![]() 面积的最大值为
面积的最大值为![]() ,
,
由![]() 得
得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某公园的门票价格如下表:
购票人数 | 1-50人 | 51-100人 | 100人以上 |
每人门票数 | 13元 | 11元 | 9元 |
实验学校初二(1)、二(2)两个班的学生共104人去公园游玩,其中二(1)班的人数不到50人,二(2)班的人数有50多人,经估算,如果两个班都以班为单位分别购票,则一共应付1240元,如果两班联合起来,作为一个团体购票,则可节省不少钱,你能否求出两个班共有多少名学生联合起来购票能省多少钱?