题目内容
【题目】已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧
(1)若AB=18,DE=8,线段DE在线段AB上移动
①如图1,当E为BC中点时,求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,求AD的长;
(2)若AB=2DE,线段DE在直线AB上移动,且满足关系式![]() ,则
,则![]() ______.
______.
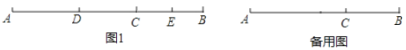
【答案】(1)①7;②3或5;(2)![]() .
.
【解析】
(1)①根据AB的长和![]() 可求出AC和BC,根据中点的定义可得CE,再由
可求出AC和BC,根据中点的定义可得CE,再由![]() 可得CD,最后根据
可得CD,最后根据![]() 计算即可得;
计算即可得;
②设![]() ,因点F(异于A、B、C点)在线段AB上,
,因点F(异于A、B、C点)在线段AB上,![]() 可知
可知![]() ,
,![]() 和
和![]() ,所以需分2种情况进行讨论:
,所以需分2种情况进行讨论:![]() 和
和![]() ,如图2、3(见解析),先根据已知条件判断点E、F位置,再将EF和CE用含x的式子表示出来,最后代入
,如图2、3(见解析),先根据已知条件判断点E、F位置,再将EF和CE用含x的式子表示出来,最后代入![]() 求解即可;
求解即可;
(2)设![]() ,先判断出DE在AB上的位置,再根据
,先判断出DE在AB上的位置,再根据![]() 得出x和y满足的等式,然后将其代入
得出x和y满足的等式,然后将其代入![]() 化简即可得.
化简即可得.
(1)①![]()
![]()
又![]() E为BC中点
E为BC中点
![]()
![]()
![]()
![]() ;
;
②设![]() ,因点F(异于A、B、C点)在线段AB上,
,因点F(异于A、B、C点)在线段AB上,![]() 可知:
可知:
![]() ,
,![]() 和
和![]()
当![]() 时,
时,![]()
![]()
![]()
![]()
此时可画图如图2所示,代入![]() 得:
得:![]()
解得:![]() ,即AD的长为3
,即AD的长为3
当![]() 时,
时,![]()
![]()
![]()
![]()
此时可画图如图3所示,代入![]() 得:
得:![]()
解得:![]() ,即AD的长为5
,即AD的长为5
综上,所求的AD的长为3或5;
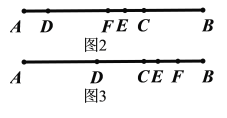
(2)①若DE在如图4的位置
设![]() ,则
,则![]()
![]()
又![]()
![]()
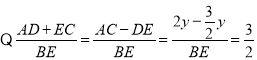
![]() (不符题设,舍去)
(不符题设,舍去)
②如DE在如图5的位置
设![]() ,则
,则![]()
![]()
又![]()
![]()
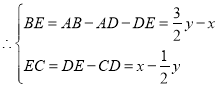
代入![]() 得:
得: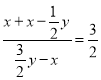
解得:![]()
则![]() .
.
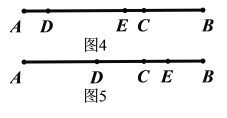

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目