题目内容

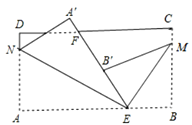
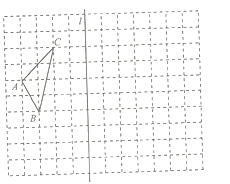
【题目】如图，在的正方形网格中，是格点三角形，点的坐标分别为，.

(1)在图中画出相应的平面直角坐标系；

(2)画出关于直线对称的，并标出点的坐标；

(3)若点在内，其关于直线的对称点是，则的坐标是 .

【答案】(1)见解析；(2)见解析，；(3)．

【解析】

（1）根据点B和点C的坐标可得坐标系；
（2）利用关于直线对称点的性质得出对应点位置进而得出答案；
（3）根据直线l经过点（-2，0），点P（a，b）关于直线l的对称点为P1，则P与P1的横坐标的和除以2等于-2，纵坐标相等，进而得出答案．

(1)如图，建立平面直角坐标系．

(2)如图，就是所画的图形，标出点的坐标

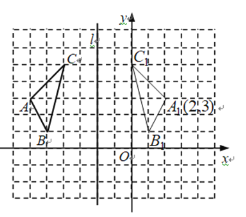
(3)点P（a，b）关于直线l的对称点为P1，则点P1的坐标是（-a-4，b）．

练习册系列答案
相关题目

【题目】某校学生会调查了八年级部分学生对“垃圾分类”的了解程度（1）在确定调查方式时，学生会设计了以下三种方案，其中最具有代表性

的方案是________；

方案一：调查八年级部分男生；

方案二：调查八年级部分女生；

方案三：到八年级每个班去随机调查一定数量的学生．

（2）学生会采用最具有代表性的方案进行调查后，将收集到的数据绘制成如下两幅不完整的统计图，如图①、图②.请你根据图中信息，回答下列问题：

①本次调查学生人数共有_______名；

②补全图①中的条形统计图，图②中了解一点的圆心角度数为_______；

③根据本次调查，估计该校八年级500名学生中，比较了解“垃圾分类”的学生大约有_______名.

【题目】如图，在平面直角坐标系中，抛物线与轴交于点，与轴交于两点，其对称轴与轴交于点.

（1）求抛物线的解析式和对称轴；

（2）在抛物线的对称轴上是否存在一点，使的周长最小？若存在，请求出点的坐标；若不存在，请说明理由；

（3）连接，在直线的下方的抛物线上，是否存在一点，使的面积最大？若存在，请求出点的坐标；若不存在，请说明理由.

【题目】如图，长方形纸片ABCD，点E，F分别在边AB，CD上，连接EF，将∠BEF对折 B落在直线EF上的点B′处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A′得折痕EN，若∠BEM＝62°15′ ，则∠AEN＝_____________．

【题目】1876年，美国总统Garfield用如图所示的两个全等的直角三角形证明了勾股定理，若图中，，，则下面结论错误的是( )

A. B. C. D. 是等腰直角三角形

【题目】如图，在△ABD中，AC⊥BD于点C， ，点E是AB的中点，tanD＝2，CE＝1，求sin∠ECB的值和AD的长．

【题目】如图，已知四边形ABCD内接于⊙O，A是的中点，AE⊥AC于A，与⊙O及CB的延长线交于点F，E，且.

(1)求证：△ADC∽△EBA；

(2)如果AB＝8，CD＝5，求tan∠CAD的值．

【题目】如图，在平面直角坐标系中，抛物线y=﹣x2+ax+b交x轴于A（1，0），B（3，0）两点，点P是抛物线上在第一象限内的一点，直线BP与y轴相交于点C．

（1）求抛物线y=﹣x2+ax+b的解析式；

（2）当点P是线段BC的中点时，求点P的坐标；

（3）在（2）的条件下，求sin∠OCB的值．

【答案】(1) y=﹣x2+4x﹣3；(2) 点P的坐标为（，）；(3) .

【解析】分析：（1）将点A、B代入抛物线y=-x2+ax+b，解得a，b可得解析式；

（2）由C点横坐标为0可得P点横坐标，将P点横坐标代入（1）中抛物线解析式，易得P点坐标；

（3）由P点的坐标可得C点坐标，A、B、C的坐标，利用勾股定理可得BC长，利用sin∠OCB=可得结果．

详解：（1）将点A、B代入抛物线y=﹣x2+ax+b可得，

，

解得，a=4，b=﹣3，

∴抛物线的解析式为：y=﹣x2+4x﹣3；

（2）∵点C在y轴上，

所以C点横坐标x=0，

∵点P是线段BC的中点，

∴点P横坐标xP==，

∵点P在抛物线y=﹣x2+4x﹣3上，

∴yP=﹣3=，

∴点P的坐标为（，）；

（3）∵点P的坐标为（，），点P是线段BC的中点，

∴点C的纵坐标为2×﹣0=，

∴点C的坐标为（0，），

∴BC==，

∴sin∠OCB===．

点睛：本题主要考查了待定系数法求二次函数解析式，二次函数图像与性质，解直角三角形，勾股定理，利用中点求得点P的坐标是解答此题的关键．

【题型】解答题
【结束】
24

【题目】如图，⊙O是△ABC的外接圆，BC是⊙O的直径，∠ABC=30°，过点B作⊙O的切线BD，与CA的延长线交于点D，与半径AO的延长线交于点E，过点A作⊙O的切线AF，与直径BC的延长线交于点F．

（1）求证：△ACF∽△DAE；

（2）若S△AOC=，求DE的长；

（3）连接EF，求证：EF是⊙O的切线．

【题目】如图，矩形ABCD的面积为20cm2，对角线交于点O；以AB、AO为邻边做平行四边形AOC1B，对角线交于点O1；以AB、AO1为邻边做平行四边形AO1C2B；…依此类推，则平行四边形AO4C5B的面积为（ ）

A. cm2 B. cm2 C. cm2 D. cm2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网