题目内容
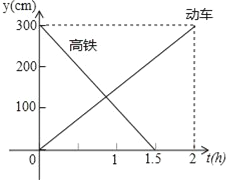
【题目】如图,一辆动车从A地开往B地,一辆高铁从B地开往A地.两车同时出发,设动车离A地的距离为y1(km),高铁离A地的距离为y2(km),动车行驶时间为t(h),变量y1、y2之间的关系图象如图所示:
(1)根据图象,求高铁和动车的速度;
(2)动车出发多少小时与高铁相遇;
(3)两车出发经过多长时间相距50km.
【答案】(1)高铁的速度为200km/h,动车的速度为150km/h;(2)动车出发![]() 小时与高铁相遇;(3)当x=1或
小时与高铁相遇;(3)当x=1或![]() 时两车相距50km.
时两车相距50km.
【解析】试题分析:(1)由题意结合图,即可得出速度;
(2)先分别求出解析式,然后联立组成方程组,解方程组即可得;
(3)将(2)中得到的两个解析式互相减即可得.
试题解析:(1)高铁的速度为:300÷1.5=200(km/h),
动车的速度为:300÷2=150(km/h).
(2)设高铁的函数解析式为:y1=kx+b,
把(0,300),(1.5,0)代入y=kx+b得: ![]() ,
,
解得: ![]() ,则y1=﹣200x+300,
,则y1=﹣200x+300,
动车的函数解析式为:y2=150x,
当动车与高铁相遇时,即﹣200x+300=150x
解得:x=![]() .
.
答:动车出发![]() 小时与高铁相遇;
小时与高铁相遇;
(3)当y1=y2时,两车相遇,解得x=![]() ,
,
①0≤x≤![]() 时,y1﹣y2=﹣200x+300﹣150x=50,得:x=
时,y1﹣y2=﹣200x+300﹣150x=50,得:x=![]() ,
,
②![]() <x≤1.5时,y2﹣y1=150x﹣(﹣200x+300)=50,得:x=1,
<x≤1.5时,y2﹣y1=150x﹣(﹣200x+300)=50,得:x=1,
综上所述:当x=1或![]() 时两车相距50km.
时两车相距50km.

练习册系列答案
相关题目
