题目内容
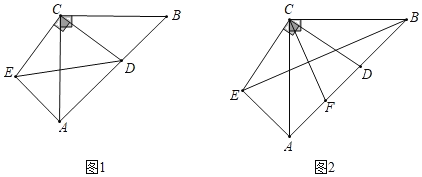
【题目】如图1.在△ABC中,∠ACB=90°,AC=BC,D为AB上一点,连接CD,将CD绕点C顺时针旋转90°至CE,连接AE.
(1)连接ED,若CD=3,AE=4,求AB的长;
(2)如图2,若点F为AD的中点,连接EB、CF,求证:CF⊥EB.
【答案】(1)AB=![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据旋转的性质,得出△BCD≌△ACE,进而得到AE=BD=4,∠CAE=∠B=45°=∠CAB,∠EAD=90°,再根据CD2+EC2=DE2=AE2+AD2,即可得到AD的长,进而求出AB的长;
(2)如图2,过C作CG⊥AB于G,则AG=BG,根据等腰直角三角形的性质可得,![]() ,再根据点F是AD的中点,可得到
,再根据点F是AD的中点,可得到![]() ,再根据
,再根据![]() ,∠CGF=∠BAE=90°,即可判定△CGF∽△BAE,进而得到∠FCG=∠ABE,依据∠ABE+∠CFG=90°,可得CF⊥BE.
,∠CGF=∠BAE=90°,即可判定△CGF∽△BAE,进而得到∠FCG=∠ABE,依据∠ABE+∠CFG=90°,可得CF⊥BE.
(1)如图1,由旋转可得:EC=DC=3,∠ECD=90°=∠ACB,
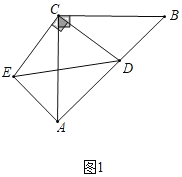
∴∠BCD=∠ACE,
又∵AC=BC,
∴△BCD≌△ACE(SAS),
∴AE=BD=4,∠CAE=∠B=45°=∠CAB,
∴∠EAD=90°,
∴DE=![]() =3
=3![]() ,
,
∴AD=![]() =
=![]() =
=![]() ,
,
∴AB=AD+BD=![]() +4.
+4.
(2)如图2,过C作CG⊥AB于G,则AG=![]() AB,
AB,
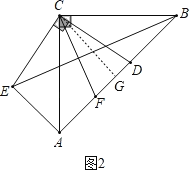
∵∠ACB=90°,AC=BC,
∴CG=![]() AB,即
AB,即![]() .
.
∵点F为AD的中点,
∴FA=![]() AD,
AD,
∴FG=AG﹣AF=![]() AB﹣
AB﹣![]() AD=
AD=![]() (AB﹣AD)=
(AB﹣AD)=![]() BD,
BD,
由(1)可得:BD=AE,
∴FG=![]() AE,即
AE,即![]() ,
,
∴![]() ,
,
又∵∠CGF=∠BAE=90°,
∴△CGF∽△BAE,
∴∠FCG=∠ABE.
∵∠FCG+∠CFG=90°,
∴∠ABE+∠CFG=90°,
∴CF⊥BE.

【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量是售价的一次函数,且相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是( )元;
(2)求月销量y与售价x的一次函数关系式:
(3)设销售该运动服的月利润为W元,那么售价为多少元时,当月的利润最大?最大利润是多少元?