Question

【题目】（本小题满分10分）

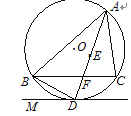
如图，点E是△ABC的内心，AE的延长线交BC于点F，交△ABC的外接圆⊙O于点D；连接BD，过点D作直线DM，使∠BDM＝∠DAC．

（1）求证：直线DM是⊙O的切线；

（2）求证：DE2＝DF·DA．

Answer 1

【答案】详见解析.

【解析】

试题分析：（1）连接DO，并延长交⊙O于点G，连接BG；易证∠BAD＝∠DAC；根据圆周角定理可得∠G＝∠BAD；即可得∠MDB＝∠G；由∠G＋∠BDG＝90°，∠MDB＋∠BDG＝90°即可得直线DM是⊙O的切线；（2）连接BE，先证∠EBD＝∠BED，即可得DB＝DE，再证△DBF∽△DAB，根据相似三角形的性质可得BD2＝DF·DA，所以DE2＝DF·DA．

试题解析：

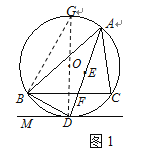
证明：（1）如图1，连接DO，并延长交⊙O于点G，连接BG；

∵点E是△ABC的内心，∴AD平分∠BAC，∴∠BAD＝∠DAC．

∵∠G＝∠BAD，∴∠MDB＝∠G，

∵DG为⊙O的直径，∴∠GBD＝90°，∴∠G＋∠BDG＝90°．

∴∠MDB＋∠BDG＝90°．∴直线DM是⊙O的切线；

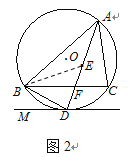
（2）如图2，连接BE．

∵点E是△ABC的内心，

∴∠ABE＝∠CBE，∠BAD＝∠CAD．

∵∠EBD＝∠CBE＋∠CBD，∠BED＝∠ABE＋∠BAD，∠CBD＝∠CAD．

∴∠EBD＝∠BED，

∴DB＝DE．

∵∠CBD＝∠BAD，∠ADB＝∠ADB，

∴△DBF∽△DAB，

∴BD2＝DF·DA．

∴DE2＝DF·DA．