题目内容
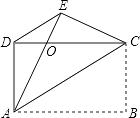
【题目】如图,△ABC的两条中线AM、BN相交于点O,已知△ABC的面积为14,△BOM的面积为3,求四边形MCNO的面积. 
【答案】解:∵△ABC的两条中线AM、BN相交于点O, ∴△BCN的面积=△ABC的面积的一半,
又∵△ABC的面积为14,
∴△BCN的面积=7,
又∵△BOM的面积为3,
∴四边形MCNO的面积=7﹣3=4.
【解析】先根据三角形的中线将三角形的面积分成相等的两部分,求得△BCN的面积,再根据△BOM的面积为3,求得四边形MCNO的面积.
【考点精析】通过灵活运用三角形的“三线”和三角形的面积,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内;三角形的面积=1/2×底×高即可以解答此题.

练习册系列答案
相关题目